Bài soạn Đại số 9 - Tiết 1 đến tiết 36 - Trưng THCS xã HiƯp Tng
I/ Mục tiêu
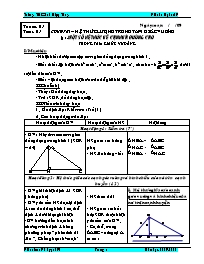
- Nhận biết được các cặp tam giác đồng dạng trong hình 1 .
- Biết thiết lập hệ thức b2 = ab, c2 = ac, h2 = bc , ah = bc và dưới sự dẫn dắt của GV.
- Biết vận dụng các hệ thức trên để giải bài tập .
II/ Chuẩn bị
- Thầy: Đồ dùng dạy học .
- Trò : SGK, đồ dùng học tập.
III/ Tiến trình dạy học
1. Ổn định lớp: Kiểm tra sĩ số(1')
2. Các hoạt đông trên lớp:
Bạn đang xem 20 trang mẫu của tài liệu "Bài soạn Đại số 9 - Tiết 1 đến tiết 36 - Trưng THCS xã HiƯp Tng", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Tuần: 01 Tiết: 01 Ngày soạn: / / 09 CHƯƠNG I – HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG §1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG I/ Mục tiêu - Nhận biết được các cặp tam giác đồng dạng trong hình 1 . - Biết thiết lập hệ thức b2 = ab’, c2 = ac’, h2 = b’c’ , ah = bc và dưới sự dẫn dắt của GV. - Biết vận dụng các hệ thức trên để giải bài tập . II/ Chuẩn bị - Thầy: Đồ dùng dạy học . - Trò : SGK, đồ dùng học tập. III/ Tiến trình dạy học Ổn định lớp: Kiểm tra sĩ số(1') 2. Các hoạt đôïng trên lớp: Hoạt động của GV Hoạt động của HS Nội dung Hoạt động 1 : Kiểm tra (7') - GV : Hãy tìm các tam giác đồng dạng trong hình 1 (SGK – 64) A B H C HS quan sát bảng phụ - HS lên bảng viết ΔHBA ΔABC ΔHAC ΔABC ΔHBA ΔHAC Hoạt đông 2 : Hệ thức giữa các cạnh góc vuông và hình chiếu của nó trên cạnh huyền (12') - GV giới thiệu định lí 1 SGK ( bảng phụ) - GV yêu cầu HS đọc lại định lí sau đó dùng hình 1 cụ thể định lí dưới dạng kí hiệu -GV hướng dẫn học sinh chứng minh định lí bằng phương pháp “ phân tích đi lên “. Chẳng hạn : b2 = a.b’ Ü Ü Ü ΔHAC ΔHAC . Sau đó giáo viên trình bày chứng minh như SGK . - GV gọi ý để HS quan sát và nhận xét được a = b’ + c’ rồi cho HS tính b2 + c2 ? Sau đó lưu ý HS có thể coi đây là một cách chứng minh khác của định lí Pi-ta-go. - HS theo dõi - HS quan sát kết hợp SGK thực hiện yêu cầu của GV. - Cụ thể , trong ΔABC vuông tại A ta có : b2 = a.b’; c2=a.c’(1) HS theo dõi. HS theo dõi thực hiện yêu cầu của GV. - Ta có : b2 + c2 = ab’ + ac’ = a(b’ + c’) = a.a = a2 1. Hệ thức giữa các cạnh góc vuông và hình chiếu của nó trên cạnh huyền Định lí 1 Trong tam giác vuông, bình phương mỗi cạnh góc vuông băng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền . ΔABC vuông tại A ta có : b2 = a.b’ ; c2 = a. c’ (1) Hoạt động 3 : Một số hệ thức liên quan đến đường cao – Định lí 2(15') - GV giới thiệu định lí 2 SGK - GV yêu cầu học sinh cụ thể hoá định lí với quy ước ở hình 1 - GV cho HS làm ?1. Bắt đầu từ kết luận, dùng “Phân tích đi lên” để xác định được cần chứng minh hai tam giác vuông nào đồng dạng .Từ đó HS thấy được yêu cầu chứng minh DAHB DCHA trong ?1 là hợp lý. - GV trình bày ví dụ 2 như SGK và giải thích để HS hiểu được cơ sở của việc tính như vậy - HS theo dõi. - HS quan sát hình 1 và trả lời HS thực hiện ?1 theo nhóm. - HS theo dõi kết hợp xem SGK. Định lí 2 Trong một tam giác vuông, bình phường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền . - Ta có : h2 = b’.c’ (2) ?1 Ta có : DAHB DCHA vì (Cùng phụ với góc ABH) Do đó : , suy ra AH2 = HB.HC Hay h2 = b’.c’ Hoạt động 4 : Củng cố ( 8' ) Yêu cầu HS nhắc lại định lý đã học? - GV gọi học sinh lên bảng làm bài tập 1, 2 (SGK – 68). - GV theo dõi hướng dẫn HS phát biểu định lý. 4 HS lên bảng thực hiện. Cả lớp làm vào vở. 1/ Bài tập 1 a/ x + y = 10; 62 = x.(x + y) Suy ra x = 3,6 ; y = 6,4 b/ 122 = x.20 Û x = 7,2 2/ Bài tập 2 x2 = 1(1 + 4) = 5 Þ x =. y2 = 4(1 + 4 )=20Þx = Hoạt động 5 : Hướng dẫn học ở nhà (2) - Học kĩ các định lí 1, định lí 2 - BTVN : 1,2 (SBT – 89) - Xem phần kế tiếp IV/ Một số lưu ý: Tuần : 03 Tiết: 02 Ngày soạn: / / 09 §1. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (TT) I/ Mục tiêu - Củng cố định lí 1 và 2 về cạnh và đường cao trong tam giác vuông. - HS thiết lập các hệ thức bc = ah và dưới sự hướng dẫn của GV. - Biết vận dụng các hệ thức trên để giải bài tập. II/ Chuẩn bị - Thầy : Giáo án, đồ dùng dạy học - Trò : SGK, xem trước bài ở nhà. - Phương pháp: thuyết trình, vấn đáp gợi mở giải quyết vấn đề. III/ Tiến trình dạy học Ổn định lớp: Kiểm tra sĩ số(1') 2. Các hoạt đôïng trên lớp: Hoạt động của GV Hoạt động của HS Nội dung Hoạt động 1 : Kiểm tra (5') - Hãy phát biểu định lí 1, định lý 2 ? - HS lên bảng trả lời Hoạt động 2 : Một số hệ thức liên quan đến đường cao – Định lí 3 (11') - GV yêu cầu học sinh cụ thể hoá định lí với quy ước ở hình 1 . - GV yêu cầu HS làm ?2 để chứng minh hệ thức (3) nhờ tam giác đồng dạng . GV hướng dẫn HS tìm cách chứng minh định lí bằng phương pháp “ Phân tích đi lên” . Qua đó rèn luyên cho HS phương pháp giải toán thường dùng. - HS sau khi đọc lại định lí dùng kí hiệu cụ thể định lí - Ta có DABC DHBA (Vì chúng có chung hóc nhọn) - Do đó , AC.BA =BC.HA Tức là b.c = a.h Định lí 3 Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng . b.c = a.h Hoạt động 3 : Một số hệ thức liên quan đến đường cao – Định lí 4(11') - GV hướng dẫn HS biến đổi từ hệ thức cần chứng minh để đến được hệ thức đẵ có như sau : ah = bc Þ a2h2 = b2c2 Þ Þ Þ Þ -Sau khi biến đổi từ hệ thức(3)được kết quả, GV yêu cầu HS phát biểu thành định lí 4. - GV thực hiện ví dụ 3 SGK như bài tập mẫu để HS theo dõi áp dụng làm các bài tập tương tự . - GV giới thiệu chú ý SGK - HS chú ý theo dõi - HS đứng tại chỗ phát biểu. - HS theo dõi GV thực hiện kết hợp xem SGK Định lí 4 Trong tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông. Ví dụ 3: Sgk Chú ý: Sgk Hoạt động 4 : Củng cố (15') - GV cho HS làm các bài tập 3, 4 (SGK – 69) 1/ Bài tập 3 y = ; xy = 5.7 = 35 suy ra x = 2/ Bài tập 4 22 = 1.x Û x = 4 y2 = x(1 + x) = 4(1 + 4) = 20 Þ Hoạt động 5 : Hướng dẫn học ở nhà (2') - Học kĩ các định lí và định nghĩa - BTVN : 5, 6, 7, 8, 9 (SGK – 89) IV/ Một số lưu ý: Tuần: 03 Ngày soạn: / / 09 Tiết: 03 LUYỆN TẬP I/ Mục tiêu - Củng cố các hệ thức về cạnh và đường cao trong tam giác vuông . - Biết vận dụng các hệ thức trện để giải bài tập II/ Chuẩn bị - Thầy : Bảng phụ, thước thẳng, compa, êke, phấn màu - Trò:Ôn tập các kiến thức đã học, thước thẳng, compa, êke, bảng nhóm, bút da - Phương pháp: Thuyết trình, vấn đáp gợi mở dẫn dắt giải quyết vấn đề. III/ Tiến trình dạy học Ổn định lớp: Kiểm tra sĩ số(1') 2. Các hoạt đôïng trên lớp: Hoạt động của GV Hoạt động của HS Nội dung Hoạt động 1: Kiểm tra - Chữa bài tập 4a SBT, sau đó phát biểu định lý áp dụng để giải bài tập đó? - Chữa bài tập 3a SBT, sau đó phát biểu định lý áp dụng để giải bài tập đó? - GV nhận xét ghi điểm. HS1 lên bảng chữa bài tập 4a, phát biểu định lý 1,2. HS2 lên bảng chữa bài tập 3a, phát biểu định lý 3, định lý Py ta go. Bài tập 4a SBT: x = 4,5; y= 5,41 Bài tập 3a SBT Hoạt động 2: Luyện tập GV yêu ccầu HS đọc đề, gọi HS lên bảng vẽ hình Để tính AH ta sử dụng công thức nào? Ta cần biết thêm yếu tố nào? Hãy nêu cách tính BC? Gọi HS lên bảng tính BC sau đó tính AH. Gọi HS lên bảng tính HC, HB? GV theo dõi GV đưa đề bài lên bảng phụ. GV vẽ hình và hướng dẫn. Gv: Tam giác ABC là tam giác gì? Vì sao? Căn cứ vào đâu có x2 =a.b. GV hướng dẫn HS vẽ hình 9 Sgk. GV: Tương tự như trên tam giác DEF là tam giác vuông vì trung tuyến OD ứng với cạnh EF và bằng nữa cạnh ấy, vậy tại sao có x2 = a.b? - Cho HS hoạt động nhóm, nữa lớp làm bài tập 8b, nữa lớp làm bài tập 8c. GV theo dõi các nhóm làm việc. - Sau thời gian hoạt động khoảng 5' GV yêu cầu đại diện 2 nhóm lêm bảng trình bài. GV kiểm tra bài làm của một vài nhóm nữa. GV đưa bảng phụ đề bài bài 9 lên bảng. GV hướng dẫn gọi 1 HS lên bảng vẽ hình. Để chứng minh DIL cân ta cần chứng minh đề gì? Tại sao DI = DL. Gv gọi HS lên bảng chứng minh GV: không đổi có nghĩa là gì? Hãy dựa vào câu a) để chứng minh câu b) HS đọc đề. 1 HS lên bảng vẽ hình. HS: AH.BC = AB.AC HS: Ta cần tính được BC HS phát biểu HS lên bảng thực hiện. Cả lớp thực hiện vào vở. HS vẽ từng hình để hiểu rõ bài toán. HS đứng tại chỗ trả lời. HS đứng tại chỗ trả lời. HS vẽ hình theo hướng dẫn của GV. HS nghe hướng dẫn. HS trả lời câu hỏi của GV. HS hoạt động theo nhóm. Đại diện hai nhóm lần lượt lên trình bày. HS nhận xét góp ý. HS vẽ hình vào vởû. 1HS lên bảng vẽ hình. HS: Để chứng minh DIL là tam giác cân, ta sẽ chứng minh DI = DL. 1 HS lên bảng chứng minh cả lớp thực hiện vào vở. HS: bằng đại lượng không đổi. HS lên bảng thực hiện. 1/Bài tập 5 H Tam giác ABC vuông tại A có AB = 3, AC = 4. theo định lí Pi-ta-go ù : BC2 = AB2 + AC2 suy ra BC = 5 mặt khác AB2 = BH.BC, suy ra BH = = = 1,8; CH = BC – BH = 5 – 1,8 = 3,2 Ta có AH.BC = AB.AC, suy ra AH = == 2,4 2/Bài tập7: Sgk-69 Cách1: Hình 8 Sgk vuông vì trung tuyến OA ứng với cạnh BC và bằng nửa cạnh ấy. Trong tam giác vuông ABC có AHBC nên AH2 = BH. HC (hệ thức 2) hay x2 = a.b. Cách 2 :(hình 9 Sgk ) Trong tam giác vuông DEF có DI là đường cao nên: DE2 = EF.EI ( hệ thức I) Hay x2 =a.b 3/Bài tập 8: b,c A y y x B x H x C b/ Do các tam giác tạo thành đều là tam giác vuông cân nên x = 2 và y = D E y 12 16 F x c/ 122 = x.16 Þ x = = 9; y2 = 122 + x2 Þy = =15 4/Bài tập 9: Sgk -70 K B C L I A D Hai tam giác vuông ADI và CDL có AD = CD ( Vì cùng phụ với góc CDI). Do đó chúng bằng nhau, suy ra DI = DL b/ Theo câu a ta có: =(1) Mặt khác trong tam giác vuông DKL có DC là đường cao ứng với cạnh huyền KL, do đó = (Không đổi) Tức là không đổi khi I thay đổi trên cạnh AB Hoạt động 3 : Củng cố - Nhắc lại các định nghĩa và định lí đã học - Chú ý khi vận dụng giải các bài toán . Hoạt động 4 : Hướng dẫn học ở nhà - Học kĩ các định nghĩa và định lí - BTVN 6, 12 trang 90,91 Sgk; 8,9,10,15,17 (SBT – 90,91) - Tiết sau tiếp tục luyện tập IV / Một số lưu ý Tuần: 03 Ngày soạn / / 09 Tiết : 04 LUYỆN TẬP (tt) I/ Mục tiêu - Củng cố các hệ thức về cạnh và đường cao trong tam giác vuông . - Biết vận dụng các hệ thức trên để giải bài tập. - Vận dụng kiuến thức đ ... Tính độ dài OA. Đáp án – Thang điểm Phần I: Trắc nghiệm: Câu 1: Mỗi đáp án đúng 0, 25 điểm x 4 = 1,0 điểm 2 3 B C Câu 3: Mỗi đáp án đúng 0, 25 điểm x 4 = 1,0 điểm 1 --> c 2 --> e 3 --> a 4--> b Phần II: Tự luận Câu Đáp án Thang điểm 3 a) Đường thẳng y = 2x + 3 song song với đồ thị hàm số y = 2x khi m = 2 b) Vẽ đồ thị hàm số d: + Vẽ hệ trục toạ độ và biểu diễn điểm + Vẽ đường thẳng d. c) tg = 2 630 26' 0,75 đ 0,5 đ 0,25 đ 0,5 đ 4 Chứng minh AD là tiếp tuyến của (O). Gọi M là giao điểm của AO và DC. Tam giác DOC cân tại O, OM là đường cao nên ODM = OCM (c.g.c) nên = 900 Do đĩAD cũng là tiếp tuyến của đường trịn (O). CM == 12 (cm) . Xét tam giác vuơng OCM, tính được OM = 9 (cm) Tam giác OAC vuơng tại C, đườmh cao CM nêm OC2 =OM.OA. Từ đĩ tính được OA =25 cm 0,5 đ 0,5 đ 0,5 đ 0,5 đ 0,5 đ 0,5 đ H§ 3: NhËn xÐt ( 8’) ¦u ®iĨm : C¸c em ®· n¾m ch¾c ®ỵc c¸c kiÕn thøc c¬ b¶n. VËn dơng tèt vµo c¸c bµi to¸n ®Ị yªu cÇu lµm . Nhỵc ®iĨm : + Cßn mét sè em cha biÕt c¸ch tr×nh bµy lêi gi¶i mét c¸ch khoa häc , ®ĩng tr×nh tù trong bµi KÕt qu¶ : Líp 9A ; tỉng sè bµi : 29 bµi . Trong ®ã : Giỏi: 6 Khá: 7 TB: 5 Yếu: 11 - TØ lƯ : 62,06 % trªn trung b×nh . KÕt qu¶ : Líp 9B ; tỉng sè bµi : 28 bµi . Trong ®ã : Giỏi: 4 Khá: 5 TB: 7 Yếu: 10 Kém: 2 - TØ lƯ : 57,14 % trªn trung b×nh . Tuần: 19 Tiết: 35 ¤n tËp ch¬ng II I. Mơc tiªu: + H/s «n tËp c¸c kiÕn thøc ®· häc ch¬ng 2 vỊ tÝnh chÊt ®èi xøngcđa ®.trßn, liªn hƯ gi÷a d©y vµ kho¶ng c¸ch tõ d©y ®Õn t©m. vÞ trÝ t¬ng ®èi cđa ®th¼ng vµ ®trßn, vÞ trÝ t® cđa 2 ®trßn. + VËn dơng ®ỵc c¸c kiÕn thøc ®· häc vµo bµi tËp vỊ tÝnh to¸n vµ chøng minh. H/s biÕt ph©n tÝch, t×m lêi gi¶i vµ tr×nh bµy lêi gi¶i, lµm quen víi d¹ng bµi t×m vÞ trÝ cđa 1 ®iĨm ®Ĩ 1 ®o¹n th¼ng cã ®é dµi lín nhÊt. + HS cã ý thøc tù «n tËp. II. chuÈn bÞ: - ThÇy: C¸c c©u hái «n tËp, - Trß : «n kiÕn thøc theo H§VN giê tríc. III. TiÕn tr×nh d¹y häc: ỉn ®Þnh tỉ chøc: C¸c ho¹t ®éng: Hoạt động của Gv Hoạt động của HS Nội dung H§ 1: ¤n tËp lý thuyÕt, kÕt hỵp kiĨm tra bµi h.s (25') C©u 1: Nèi víi « ë cét tr¸i víi 1 « ë cét ph¶i ®Ĩ ®ỵc k.®Þnh ®ĩng? I. Lý thuyÕt. C©u 1: 1-b ; 2-g ; 3-d ; 4-e ; 5-a ; 6-c 1. §.trßn ngo¹i tiÕp 1 tam gi¸c. 2. §trßn néi tiÕp 1 tam gi¸c. 3. T©m ®.xøng cđa ®trßn. 4. Trơc ®x cđa ®trßn. 5. T©m cđa ®trßn néi tiÕp tg. 6. T©m cđa ®trßn ngo¹i tiÕp tg. a. lµ g® cđa ®êng ph©n gi¸c trong tam gi¸c. b. lµ ®trßn ®i qua 3 ®Ønh cđa tam gi¸c. c.lµ g® cđa c¸c ®êng tt c¸c c¹nh tg'. d. chÝnh lµ t©m cđa ®trßn. e. lµ bÊt kú ®k nµo cđa ®trßn. g. lµ ®êng trßn tiÕp xĩc víi tÊt c¶ c¸c c¹nh cđa tam gi¸c. C©u 2: §iỊn vµo chç (..) ®Ĩ ®ỵc c¸c ®Þnh lý. 1. Trong c¸c d©y cđa 1 ®trßn, d©y lín nhÊt lµ . 2. Trong 1 ®trßn: a. §kÝnh vu«ng gãc víi 1 d©y th× ®i qua b. §kÝnh ®i qua t.®iĨm cđa 1 d©y.. th×.. c. Hai d©y b»ng nhau th× hai d©y .th× b»ng nhau d. D©y lín h¬n th× .t©m h¬n D©y .t©m h¬n th× .hpn C©u 2: 1. ®êng kÝnh 2. Trung ®iĨm cđa d©y Êy Kh«ng ®i qua t©m vu«ng gãc víi d©y Êy C¸ch ®Ịu t©m C¸ch ®Ịu t©m GÇn GÇn lín C©u 3: nªu c¸c vÞ trÝ t.®èi cđa ®th¼ng vµ ®trßn. ? ? ph¸t biĨu c¸c t/c t.t ®.trßn ? G/v chèt l¹i c¸c k.t c¬ b¶n cđa ch¬ng H/s nªu hƯ thøc t¬ng øng. H§ 2: LuyƯn tËp. Bµi 41 ( SGK – T.128) GT : Cho (O;) ;AD ^BC º H ; HE ^ AB ; HF ^ AC KL : a) x¸c ®Þnh vÞ trÝ cđa (I) vµ (O) , (K) vµ (O) , (I) vµ (K) b) Tø gi¸c AEHF lµ h×nh g× ? c) AE.AB = AF.AC d) EF ^ IE ; EF ^ KF e) H ? ®Ĩ EF lín nhÊt II. Bµi tËp. Chøng minh : a) D BEH cã (gt) IB = IH ® I lµ t©m ®êng trßn ngo¹i tiÕp D BEH . T¬ng tù KH = KC ® K lµ t©m ®êng trßn ngo¹i tiÕp D HFC . + Ta cã : IO = OB - IB ® (I) tiÕp xĩc trong víi (O) ( theo hƯ thøc liªn hƯ vỊ c¸c vÞ trÝ t¬ng ®èi cđa hai ®êng trßn ) + Ta cã : OK = OC - KC ® (K) tiÕp xĩc trong víi (O) ( hƯ thøc liªn hƯ vỊ vÞ trÝ t¬ng ®èi cđa hai ®êng trßn ) + Ta cã : IK = IH + KH ® (I) tiÕp xĩc ngoµi (K) ( theo hƯ thøc tiÕp xĩc ngoµi ) . b) Theo (gt) ta cã : (1) D ABC néi tiÕp trong (O) cã BC lµ ®êng kÝnh . L¹i cã OA = OB = OC ® ( 2) Tõ (1) vµ (2) ® tø gi¸c AEHF lµ h×nh ch÷ nhËt v× cã 3 gãc vu«ng . c) Theo (gt) ta cã D HAB vu«ng t¹i H , mµ HE ^ AB t¹i E (gt) ® Theo hƯ thøc gi÷a c¹nh vµ ®êng cao trong tam gi¸c vu«ng ta cã : AH2 = AB . AE (3) L¹i cã D AHC vu«ng t¹i H , cã HF lµ ®êng cao ® theo hƯ thøc liªn hƯ gi÷a c¹nh vµ ®êng cao trong tam gi¸c vu«ng ta cã : AH2 = AC . AF (4) Tõ (3) vµ (4) ta suy ra : AB . AE = AC . AF ( ®cpcm) d) Gäi G lµ giao ®iĨm cđa EF vµ AH . Theo ( cmt) ta cã AEHF lµ h×nh ch÷ nhËt ® GA = GH = GE = GF ( t/c hcn ) ®D GHF c©n t¹i G ® L¹i cã D KHF c©n t¹i K ® Mµ ( gt) (7) Tõ (5) , (6) , (7) ® VËy GF ^ FK ® EF ^ FK t¹i F ® EF lµ tiÕp tuyÕn cđa (K) Chøng minh t¬ng tù ta cịng cã EF ^ IE t¹i E ® EF cịng lµ tiÕp tuyÕn cđa (I) e) Theo ( cmt) ta cã tø gi¸c AEHF lµ h×nh ch÷ nhËt ® EF = AH ( t/c hcn) , mµ AH = . VËy EF lín nhÊt nÕu AD lín nhÊt . D©y AD lín nhÊt khi AD lµ ®êng kÝnh ® H trïng víi O. VËy d©y AD vu«ng gãc víi BC t¹i O th× EF cã ®é dµi lín nhÊt . - GV ra bµi tËp gäi HS ®äc ®Ị bµi , vÏ h×nh vµ ghi GT , KL cđa bµi to¸n . - GV vÏ h×nh lªn b¶ng , híng dÉn HS chøng minh . - Bµi to¸n cho g× ? yªu cÇu g× ? - §Ĩ xÐt vÞ trÝ t¬ng ®èi cđa hai ®êng trßn ta dùa vµo hƯ thøc nµo ? - Gỵi ý : Dùa vµo c¸c vÞ trÝ t¬ng ®èi cđa hai ®êng trßn vµ hƯ thøc liªn hƯ gi÷a ®êng nèi t©m vµ b¸n kÝnh . + H·y tÝnh IO = ? OB ? IB ® (I) ? (O) + Khi nµo th× hai ®êng trßn tiÕp xĩc trong ? + TÝnh OK theo OC vµ KC tõ ®ã suy ra vÞ trÝ t¬ng ®èi cđa (K) vµ (O) . - Khi nµo th× hai ®êng trßn tiÕp xĩc ngoµi ? + TÝnh IK theo IH vµ KH råi nhËn xÐt . - Cã nhËn xÐt g× vỊ D ABC ? So s¸nh OB , OC , OA råi nhËn xÐt ? - Tø gi¸c AEHF lµ h×nh g× ? v× sao ? cã mÊy gãc vu«ng ? - Theo ( cmt ) D HAB vµ HAC lµ tam gi¸c g× ? - TÝnh tÝch AB . AE vµ AC . AF sau ®ã so s¸nh . - Theo hƯ thøc liªn hƯ gi÷a c¹nh vµ ®êng cao trong tam gi¸c vu«ng® ta cã hƯ thøc nµo ? TÝch AB . AE b»ng g× ? - VËy ta cã thĨ rĩt ra ®iỊu g× ? - Gäi G lµ giao ®iĨm cđa AH vµ EF ® D nµo c©n ® c¸c gãc nµo b»ng nhau . - Gỵi ý : Chøng minh D GHF c©n ® gãc GFH = gãc GHF ; D KHF c©n ® gãc KFH = gãc KHF råi tÝnh GFK . - GV yªu cÇu HS chøng minh . - Nªu c¸ch t×m vÞ trÝ cđa H ®Ĩ EF lín nhÊt . - H·y tÝnh EF = AH = ? - EF lín nhÊt khi AD lµ d©y nh thÕ nµo ? vËy H ë vÞ trÝ nµo th× EF lín nhÊt . HS ®äc ®Ị bµi , vÏ h×nh vµ ghi GT , KL cđa bµi to¸n . HS tr¶ lêi miƯng. - Ta dùa vµo hƯ thøc gi÷a d víi R vµ r. HS tÝnh - d = R – r > 0 - d = R + r D ABC néi tiÕp trong (O) cã BC lµ ®êng kÝnh tø gi¸c AEHF lµ h×nh ch÷ nhËt v× cã 3 gãc vu«ng . AH2 = AC . AF AB . AE = AC . AF HS lµm theo gỵi ý. H§ 3: Híng dÉn vỊ nhµ. - N¾m ch¾c dÊu hiƯu nhËn biÕt tiÕp tuyÕn . C¸c vÞ trÝ t¬ng ®èi cđa hai ®êng trßn vµ hƯ thøc liªn hƯ øng víi tõng vÞ trÝ ®ã . Häc thuéc c¸c ®Þnh lý vµ tÝnh chÊt . Gi¶i bµi tËp 42 , 43 ( sgk – tr.128) Tuần: 19 Tiết: 36 ¤n tËp ch¬ng II (TiÕt 2) I. Mơc tiªu: + TiÕp tơc cđng cè c¸c kiÕn thøc ®· häc Ch¬ng 2.. + VËn dơng c¸c kiÕn thøc ®· häc vµo bµi tËp vµo tÝnh to¸n; chøng minh häc sinh biÕt vÏ h×nh; ph©n tÝch bµi to¸n, tr×nh bµy lËp luËn. + Kü n¨ng vÏ h×nh, ph©n tÝch bµi to¸n tr×nh bµy II. chuÈn bÞ: - ThÇy: thíc th¼ng; compa; phÊn mÇu. - Trß : «n tËp lý thuyÕt ch¬ng 2; h×nh häc lµm c¸c bµi tËp theo H§ giê tríc. III. TiÕn tr×nh d¹y häc: ỉn ®Þnh tỉ chøc: C¸c ho¹t ®éng: Hoạt động của Gv Hoạt động của HS Nội dung H§ 1: KiĨm tra. ? Ph¸t biĨu ®Þnh lý ®êng kÝnh vµ d©y cung (§L1;2) ? §Ĩ CM 1 ®t' lµ tiÕp tuyÕn cđa 1 ®trßn ta CM ntn? ? Ph¸t biĨu ®/lý vỊ 2 t.t c¾t nhau cđa 1 ®trßn ? Gäi h/s nhËn xÐt HS ph¸t biĨu c¸c ®Þnh lý H§ 2: LuyƯn tËp. Bµi tËp 1: cho (0 ; 20 cm) c¾t (0' ; 15cm) T¹i A ; B (0 vµ 0' n»m kh¸c phÝa ®v AB vÏ ®êng kÝnh A0E vµ ®êng kÝnh A0'F biÕt AB = 24cm a. §o¹n nèi t©m 00' cã ®é dµi lµ A. 7cm ;B. 25cm ; C. 30cm b. §o¹n EF cã ®é dµi lµ A.50cm; B.60cm ; C.20cm c. DiƯn tÝch DAEF b»ng A. 150cm2 ; B. 1200cm2 ; C.600cm2 - Cho h/s th¶o luËn nhãm ngang (3') - Y/cÇu h/s t×m kÕt qu¶ ®ĩng, gi¶i thÝch c¸ch tÝnh. - Yªu cÇu 1 h/s ®äc to ®Ị bµi - G/v HD h/sinh vÏ h×nh - Yªu cÇu H/s ghi gi¶ thiÕt kÕt luËn bµi to¸n P2 Ch/minh 1 tø gi¸c lµ hcn - §Ĩ CM tø gi¸c AEMF lµ hcn? - G/v kh¾c s©u P2 Ch/m - Y/cÇu h/s nªu c¸ch CM kh¸c ®v viƯc CM gãc E = 1v ; gãc F = 1v - Yªu cÇu h/s nªu c¸ch CM - ChØ râ kinh tÕ vËn dơng ? c. CM 00' lµ T2 cđa ®.trßn ®.kÝnh BC ? §.trßn ®kÝnh BC cã t©m ë ®©u cã ®i qua A kh«ng ? ? T¹i sao 00' lµ tiÕp tuyÕn cđa (M) ? ? §trßn ®.kÝnh 00' cã t©m n»m ë ®©u Y/c CM: M Ỵ (I) ; BC ^ IM - G/v chèt l¹i c¸c bíc Ch/m bµi to¸n. ? Ph¬ng ph¸p CM 1®t' lµ tiÕp tuyÕn ®êng trßn trong bµi. - P2 CM: HƯ thøc ®o¹n th¼ng H/s th¶o luËn nhãm ngang - KÕt qu¶ a. B. 25cm b. A. 50cm c. 600cm2 1 h/s ®äc to ®Ị bµi. H/s ghi gi¶ thiÕt kÕt luËn bµi to¸n. H/s : - T/g cã 3 gi¸o viªn - H×nh b/hµnh cã 2 ®.chÐo = nhau - H×nh b/hµnh cã 1 gãc vu«ng H/s CM: Gãc M = gãc E = gãc F =1v M0 ^ M0' ME ^ AB M0 ; M0' lµ 2pg m0 lµ T2 cđa 2 gãc kỊ bï cđa AB MB = MA 0B = 0A Gãc F = 1v CM T2 H/s nªu híng CM Sư dơng k.thøc lỵng trong Dvu«ng H/s t©m M v× MB = MC = MA ®.trßn nµy cã qua A H/s theo dâi, CM CM: BC lµ tiÕp tuyÕn cûa ®.trßn ®.kÝnh 00' H/s t©m I ; I lµ t®' cđa 00' H/s CM ®êng th¼ng ®ã vu«ng gãc b¸n kÝnh t¹i mĩt b¸n kÝnh. H/s kh¸c ¸p dơng ht liªn hƯ c¹nh vµ ®.cao trong D vu«ng. - CM: tam gi¸c ®ång d¹ng => ®pcm. Bµi tËp 1: - KÕt qu¶ a. B. 25cm b. A. 50cm c. 600cm2 Bµi 42 (SGK-128) GT: (O) tiÕp xĩc ngoµi (O') ë A tiÕp tuyÕn chung ngoµi BC ; BE (O) ; C Ỵ (O') - TiÕp tuyÕn chung trong t¹i A c¾t BC t¹i M ; OM Ç AB º E O'M Ỵ AC º F KL: a. AEMF lµ hcn b. ME.MO = MF.MO' c. OO' lµ T2 cđa ®kÝnh BC d. BC ----- OO' Ch/minh: a. Cã OM lµ ph©n gi¸c gãc BMA (t/c 2 tiÕp tuyÕn c¾t nhau) T¬ng tù M0' lµ ph©n gi¸c gãc CMA MO^MO'gãcOMO'= 900 Cã MA = MB tÝnh chÊt 2 tiÕp tuyÕn c¾t nhau OA = OB = R (O) MO lµ tuyÕn tuyÕn cđa AB MO^ABGãc MEA= 900 CM t¬ng tù cã gãc MFA = 900 VËy tø gi¸c AEMF cã 3 gãc vu«ng nªn cã lµ h×nh ch÷ nhËt b. D MAO AE ^ MO MA2= ME.MO D vu«ng MAO' cã AF ^ MO' MA2 = MF.MO Suy ra ME.MO = MF.MO' c. V× MA = MB = MC (tÝnh chÊt tiÕp tuyÕn c¾t nhau) A Ỵ (M) ®.kÝnh. Cã OO' ^ b¸n kÝnh MA OO' lµ tiÕp tuyÕn cđa (M) ®.kÝnh BC d. §trßn ®kÝnh OO' cã t©m lµ I lµ t®' cđa OO' D vu«ng OMO' cã MI lµ t/tuyÕn Ỵ c¹nh huyỊn. MI = OO'/2 M Ỵ (I) - H×nh thang OBCO' cã MI lµ ®êng TB (v× BC = MC vµ IO = IO') MI//OB mµ BC ^ 0B BC ^ IM BC lµ tiÕp tuyÕn cđa ®êng trßn ®êng kÝnh OO' H§ 3: Híng dÉn vỊ nhµ. - ¤n tËp kü c¸c kiÕn thøc ®· häc, häc thuéc c¸c kh¸i niƯm , ®Þnh nghÜa , ®Þnh lý . - Xem l¹i c¸c bµi tËp ®· ch÷a, c¸ch vËn dơng ®Þnh lý vµo chøng minh bµi to¸n . - ChuÈn bÞ kü c¸c kiÕn thøc cho «n tËp häc kú I.
Tài liệu đính kèm:
 HINH HOC 9 HKI(1).doc
HINH HOC 9 HKI(1).doc





