Bộ đề kiểm tra 1 tiết Chương I Hình học Lớp 9 (Có lời giải)

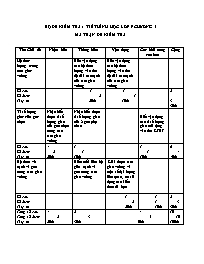
BỘ ĐỀ KIỂM TRA 1 TIẾT HÌNH HỌC LỚP 9 CHƯƠNG I
MA TRẬN ĐỀ KIỂM TRA
Tên Chủ đề 

Nhận biết
Thông hiểu
Vận dụng

Các khả năng cao hơn
Cộng
Hệ thức lượng trong tam giác vuông

Biết vận dụng các hệ thức lượng vào tìm độ dài các cạnh của tam giác vuông
Biết vận dụng các hệ thức lượng vào tìm độ dài các cạnh của tam giác vuông


Số câu 
Số điểm 
Tỉ lệ %

 1
 2
 20%
 1
 1
 10%
 
 
2
 3
30% 
Tỉ số lượng giác của góc nhọn
Nhận biết được tỉ số lượng giác của góc nhọn trong các tam giác vuông
Nhận biết được tỉ số lượng giác của 2 góc phụ nhau

Biết vận dụng các tỉ số lượng giác mở rộng vào tìm GTBT

Số câu 
Số điểm 
Tỉ lệ %
4
 2
20%
1
 1
10%

1
 1
10%
6
 4
40% 
Hệ thức về cạnh và góc trong tam giác vuông


Hiểu mối liên hệ giữa cạnh và góc trong tam giác vuông
 Giải được tam giác vuông và một số đại lượng liên quan, có sử dụng các kiến thức đã học
Số câu 
Số điểm 
Tỉ lệ %



 1
 2
 20%
 1
 1
 10%
2
 3
30%
Tổng số câu 
Tổng số điểm
Tỉ lệ %
4
 2
20%
2
 3
30%
 4
 5
 50%
10
 10
100%
ĐỀ SỐ 1
Điểm:
Lời phê của cô giáo:
Đề ra:
I) PHẦN TRẮC NGHIỆM (3 điểm) Học sinh chọn một ý đúng nhất, bằng cách khoanh vào một trong các chữ cái A, B, C, D để trả lời cho mỗi câu hỏi sau: 
Câu 1: ▲ABC vuông tại A, đường cao AH. Biết BH = 9cm, BC = 25cm, khi đó AB bằng:
A. 20cm
B. 15cm
C. 34cm
D. 25/9
Câu 2: Giá trị của biểu thức sin 36° - cos54° bằng:
A. 2 sin 36°
B. 0
C. 2 cos54° 
D. 1
Câu 3: ▲DEF vuông tại D, biết DE = 25, góc E = 42° ,thì độ dài của cạnh EF bằng bao nhiêu?
A. 18,58
B. 22,51
C. 16,72
D. Một kết quả khác.
Câu 4: ▲ABC vuông tại B , biết AB =5 , BC = 12 thì số đo của góc C bằng bao nhiêu?
A. 22°57´
B. . 20°48´
C. 24°50´
D. 23°10´ 
Câu 5: ▲OPQ vuông tại P ,đường cao PH Biết OP = 8, PQ = 15 thì PH bằng khoảng bao nhiêu?
A. 7,58
B. 5,78
C. 7,06
D. 6,07
Câu 6: Cho , ta có:
A. 
B. 
C. 
D. 




II) PHẦN TỰ LUẬN (7điểm)
Câu 1( 1đ 5) Đổi các tỉ số lượng sau đây thành tỉ số lượng giác của góc nhỏ hơn 45°
 Sin 60°31´ ; Cos 75°12´ ; Cot 80° ; Tan 57°30´ ; Sin 69°21´ ; Cot 72°25´ 
Câu 2( 4đ 5): Cho ▲ABC vuông tại A, AH là đường cao biết AB = 21cm, AC=72 cm.
 a) Giải tam giác vuông ( Độ dài lấy gần đúng 2 chữ số thập phân, góc làm tròn đến phút )
 b) Tính AH; BH ; CH.
 c) Phân giác BD của góc B ( D thuộc AH ) .Tính độ dài AD ; DH.
Câu 3( 1,0 đ): Cho ∆ABC nhọn có góc A = 60° .Chứng minh rằng : 
 
Bài làm








ĐỀ SỐ 2
I) PHẦN TRẮC NGHIỆM (3 điểm) Học sinh chọn một ý đúng nhất, bằng cách khoanh vào một trong các chữ cái A, B, C, D để trả lời cho mỗi câu hỏi sau: 
Câu 1: ▲ABC vuông tại A, đường cao AH. Biết BH = 4cm, HC = 16cm, khi đó AB bằng:
A. 8cm
B. cm
C. cm
D. 
Câu 2: Giá trị của biểu thức sin 30° - cos60° bằng:
A. 2 sin 30°
B. 2 cos60°
C. 1
D. 0
Câu 3: ▲DEF vuông tại D, biết DE = 25, góc E = 42° ,thì độ dài của cạnh EF bằng bao nhiêu?
A. 22,52
B. 27,70
C. 33,65
D. 37,31
Câu 4: ▲ABC vuông tại B , biết AB =6, AC = 7,5 thì số đo của góc C bằng bao nhiêu?
A. 36°52´
B. . 38°39´
C. 24°50´
D. 53°07´ 
Câu 5: ▲MNP vuông tại P ,đường cao PH Biết NP = 5, PM = 12thì PH bằng khoảng bao nhiêu?
A. 4,62
B. 6,42
C. 5,42
D. 4,52
Câu 6: Cho , ta có:
A. 
B.. 
C. 
D. 




II) PHẦN TỰ LUẬN (7điểm)
Câu 1( 1đ 5) Đổi các tỉ số lượng sau đây thành tỉ số lượng giác của góc nhỏ hơn 45°
 Sin 52°35´ ; Cos 64°12´ ; Cot 75° ; Tan 59°37´ ; Sin 59°11´ ; Cot 63°25´ 
Câu 2( 4đ 5): Cho ▲MNP vuông tại M, MH là đường cao biết MN =16cm, MP=30cm.
 a) Giải tam giác vuông ( Độ dài lấy gần đúng 2 chữ số thập phân, góc làm tròn đến phút )
 b) Tính MH; NH ; PH.
 c) Phân giác ND của góc N ( D thuộc MH ) .Tính độ dài MD ; DH.
Câu 3( 1,0 đ): Cho ∆ABC nhọn có góc A = 60° .Chứng minh rằng : 
ĐÁP ÁN
BÀI KIỂM TRA 1 TIẾT HÌNH HỌC CHƯƠNG I LỚP 9
 I. Phần trắc nghiệm : ĐỀ 1 & 2:( Mỗi câu cho 0,5 điểm)
 Câu 1
 Câu 2
 Câu 3
 Câu 4
 Câu 5
 Câu 6
 B
 B
 D
 A
 C
 D
 B
 D
 C
 D
 B
 B

II) Phần tự luận: Đề 1
Bài

 Lời giải
Biểu
điểm


Bài 1: ( 1đ5) 
 Cos 29°29´; Sin 14°48´ ; Tan 10°; Cot 32°30´ ; Cos 20°39´ ; Tan17°35´ 
 Mỗi tỉ số chấm 0,25đ

1, 5


a)
b)
 
Bài 2: Vẽ hình ghi GT, KL 
 Áp dụng Định lí PiTaGo trong ∆ABC ta có:
 = 212 + 722
 => BC = 75 (cm )
 Sin C = = 0,28 ( TSLG của góc nhọn )
 => góc C = 16°15´ do đó góc B = 73°45´
 Áp dụng hệ thức lượng trong ∆ABC vuông tại A ta có: 
 AH. BC = AB. AC ( đ/lí 3 ) 
 => thay số 
 = = 20.16 (cm)
 Và : AB2 = BH .BC => BH = = ( định lí 1 )
BH = 5,88 
Ta lại có: BH + HC = BC
 => HC = BC – BH = 75 – 5,88 = 69,12 (cm)
c) Áp dụng t/c đường phân giác vào ∆ABH có:
=> AD = AB.0,75 = 15,75 (cm)
 DH = AH – AD = 4,41 (cm)
0,25đ
0,5đ
0,75đ
0,25đ
0,25đ
0,5đ
0,5đ
0,75đ
0,75đ



Bài 3: 
 Kẻ đường cao BH của ∆ABC thì H nằm trên tia AC do đó :
 HC2 = ( AC – HC )2
 Áp dụng định lí PiTaGo có 
 BC2 = BH2 + HC2 
 = BH2 + ( AC – HC )2
 = BH2 + HC2 +AC2 – 2AC.AH
 = AB2 +AC2 – 2AC.AH
 Do góc BAC =60° nên AH = Cos60° =
 => BC2 = 
0,25đ
0,5đ
0,25đ
0,25đ
0,25
0,25đ
0.5đ
0,25đ

_ HS làm cách khác với suy luận hợp lí vẫn cho điểm tối đa.
_ Đáp án đề B chấm tương tự.
Bài

 Đề 2 Lời giải
Biểu
điểm


Bài 1: ( 1đ5) 
 Cos 7°25´; Sin 25°48´; Tan 25° ; Cot 30°23´ ; Cos 30°49´ ; Tan26°35´ 
 Mỗi tỉ số chấm 0,25đ

1, 5đ


a)
b)
 
Bài 2: Vẽ hình ghi GT, KL 
 Áp dụng Định lí PiTaGo trong ∆MNPta có:
 = 162 + 302
 => NP = 34 (cm )
 Sin P= = 0,47 (TSLG của góc nhọn)
 => góc P = 28°2´ do đó góc N = 62°58´
 Áp dụng hệ thức lượng trong ∆MNP vuông tại M ta có: 
 MH. NP = MN. MP (đ/lí 3) 
 => thay số 
 = = 14,12 (cm)
 Và : MN2 = NH. NP => NH = = (định lí 1)
NH = 7,53 (cm) 
Ta lại có: NH + HP = NP
 => HP = NP – NH = 34 – 7,53 = 6,59 (cm)
c) Áp dụng t/c đường phân giác vào ∆ABH có:
=> MD= MN.0,6 = 9,6 (cm)
 DH = MH – MD = 14,12- 9,6=4,52 (cm)
0,25đ
0,5đ
0,75đ
0,5đ
1đ
0,25đ
0,25đ
0,5đ
0,5đ
Bài 3: 
 Kẻ đường cao BH của ∆ABC thì H nằm trên tia AC do đó :
 HC2 = ( AC – HC )2
 Áp dụng định lí PiTaGo có 
 BC2 = BH2 + HC2 
 = BH2 + ( AC – HC )2
 = BH2 + HC2 +AC2 – 2AC.AH
 = AB2 +AC2 – 2AC.AH
 Do góc BAC =60° nên AH = Cos60° =
 => BC2 = 
0,25đ
0.5đ
0,25đ

ĐỀ SỐ 3
TRẮC NGHIỆM: Khoanh tròn chữ cái đầu câu chọn 
Câu 1: Độ dài đường cao của một tam giác đều cạnh là:
A. 	B. 	C. 	D. 
Câu 2: Một người ngồi trên tháp canh cao so với mực nước biển. Nhìn thâý một chiếc thuyền ( như hình vẽ). Khi đó chiếc thuyền cách cách tháp một khoảng (làm tròn đến hàng đơn vị) bằng :
A. 	
B. 	
C. 	
D. 
Câu 3: Một người đi xe đạp leo lên một cái dốc .Biết. Khi đó độ cao tại đỉnh và lần lượt là:
A. 	B. 	 
C. 	D. 
Câu 4: Giá trị của biểu thức bằng:
A. 	B. 	C. 	D. 
Câu 5: Giá trị của biểu thức khi là :
A. 	B. 	C. 	D. 
Câu 6: Nếu . Giá trị của bằng;
A. 	 B. C. 	 D. 
Câu 7: Tam giác có . Khi đó độ lớn của bằng:
A. Lớn hơn 	 B. Khác 	 C. Nhỏ hơn 	D. 	 
Câu 8: Xem hình vẽ. Độ dài bằng:
A. 	B. 	
C. 	D. 
Câu 9: Tam giác vuông tại , đường cao có . Khi đó bằng:
A. 	B. 	C. 	D. 
Câu 10: So sánh và , ta có;
A. không so sánh được	B. 
C. 	D. 
Câu 11: Diện tích hình bình hành có là:
A. 	B. 	C. 	D. 
Câu 12: Cho tam giác có đường trung tuyến . Khi đó bằng;
A. 	B. 	C. 	D. 
Câu 13: Xem hình vẽ. Độ dài cạnh bằng:
A. 
B. 
C. 
D. 
Câu 14: Xem hình vẽ. Độ dài bằng:
A. B. 
C. D. 
Câu 15: Giá trị của biểu thức bằng;
A. 	B. 	C. 	D. ------------------
Câu 16: Cho góc nhọn có . Khi đó giá trị của bằng;
A. 	 B. 	 C. 	 D. 
TỰ LUẬN
1/ Cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với A qua điểm B. Trên tia đối của tia HA lấy điểm E sao cho HE = 2HA. Gọi I là hình chiếu của D trên HE.
	a) Tính AB, AC, HC, biết AH = 4cm, HB = 3cm.	b) Tính .
	c) Chứng minh .	d) Chứng minh: .
2/ Cho tam giác ABC ( BA< BC) vuông tại B , đường cao BK chia cạnh huyền AC thành hai đoạn AK = 9cm; KC= 16 cm.
Tính BK
Giải tam giác vuông ABC. ( góc làm tròn đến độ) 
3 / Cho tam giác ABC vuông tại A có AB = 10cm, 
a) Tính độ dài BC?
b) Kẻ tia phân giác BD của góc ABC (D AC). Tính AD?
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ hai)
4/ Cho hình chữ nhật ABCD. Từ D hạ đường vuông góc với AC, cắt AC ở H. Biết rằng AB = 13cm; DH = 5cm. Tính độ dài BD
5/Trong tam giác ABC có AB = 12cm, B = 400, C = 300, đường cao AH. 
Hãy tính độ dài AH, HC?
6/ Cho hình thang cân ABCD ( AB//CD và AB < CD), BC = 15cm ; Đường cao BH = 12cm, DH = 16cm
Chứng minh DB vuông góc với BC
Tính diện tích hình thang ABCD
Tính BCD (làm tròn đến độ)