Đề cương ôn tập môn Toán Lớp 9 - Chuyên đề 2, Bài 5: Vị trí tương đối của hai đường tròn (Có lời giải)

Bài 5: Vị trí tương đối của hai đường tròn
A. Kiến thức cần nhớ
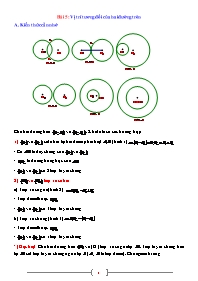
Cho hai đường tròn và . Khi đó ta có các trường hợp:
1) và cắt nhau tại hai điểm phân biệt (hình 1) 
- Có là dây chung của và 
- là đường trung trực của 
- và có 2 tiếp tuyến chung 
2) và tiếp xúc nhau
a) Tiếp xúc ngoài (hình 2) 
- Tiếp điểm thuộc 
- và có 3 tiếp tuyến chung 
b) Tiếp xúc trong (hình 3) 
- Tiếp điểm thuộc 
- và có 1 tiếp tuyến chung 
*) Đặc biệt: Cho hai đường tròn và (O’) tiếp xúc ngoài tại . Tiếp tuyến chung tròn tại cắt tiếp tuyến chung ngoài tại (, là tiếp điểm). Chứng minh rằng:
1) thẳng hàng	
2) 
3) 	
4) vuông tại 
5) vuông	
6) 
Chứng minh:
Theo tính chất 5) vuông tại 
Mà là đường cao của tam giác
Theo tính chất 3) 
3) và không có điểm chung
a) Hai đường tròn nằm ngoài nhau (hình 4) 
- và có 4 tiếp tuyến chung (2 tiếp tuyến chung trong, 2 tiếp tuyến chung ngoài)
b) Hai đường tròn đựng nhau (hình 5) 
- và không có tiếp tuyến chung
c) Hai đường tròn đồng tâm (hình 6) 
B. Bài tập vận dụng
Bài 1:
Cho hai đường tròn và cắt nhau tại và . Vẽ và theo thứ tự là đường kính của và 
a) Chứng minh rằng 3 điểm thẳng hàng
b) Đường thẳng cắt tại , đường thẳng cắt tại . Chứng minh rằng bốn điểm cùng thuộc 1 đường tròn
c) Một đường thẳng thay đổi luôn đi qua và cắt tương ứng tại sao cho nằm giữa . Xác định vị trí tương đối của đường thẳng để đạt giá trị lớn nhất. 

Lời giải
a) Ta có (góc nội tiếp chắn nửa đường tròn)
 thẳng hàng (đpcm)
b) Dễ thấy 4 điểm cùng thuộc một đường tròn đường kính (đpcm)
c) Gọi là trung điểm của ; kẻ là hình thang có là đường trung bình 
mà 
 đạt GTLN bằng 

Bài 2:
Cho và ở ngoài nhau. Kẻ tiếp tuyến chung ngoài và tiếp tuyến chung trong . Với và . Gọi là giao điểm của 
a) Chứng minh rằng:
b) Chứng minh 

Lời giải
a) là phân giác của 
Tương tự ta có là phân giác của 
Mặt khác (g-g)
b) Ta có: (phụ ), mà 
Mà (đpcm).

Bài 3:
Cho hai đường tròn và cắt nhau tại A và B. Gọi là dây cung của tiếp xúc với , là dây cung của tiếp xúc với . Gọi là điểm đối xứng của 
Qua 
a) Chứng minh rằng 4 điểm cùng thuộc 1 đường tròn
b) Chứng minh rằng: Khi hai đường tròn và thay đổi nhưng luôn đi qua 2 điểm cố định thì tâm của đường tròn đi qua bốn điểm sẽ thuộc 1 đường tròn cố định. 

Lời giải
a) Kẻ đường kính của và 
 thẳng hàng 
Gọi là trung điểm của , ta có: là trung điểm của 
Trong tam giác , có là đường trung bình 
Mà 
Tương tự ta có là đường trung bình của 
Từ (1)(2)(3) (đpcm)
b) Do , mà thuộc đường thẳng vuông góc với tại (đpcm).

Bài 4:
Cho hai đường tròn và cắt nhau tại hai điểm phân biệt và . Đường thẳng cắt và lần lượt tại và ,
 cắt và lần lượt tại và 
a) Chứng minh rằng 3 đường thẳng và đồng quy tại 
b) Chứng minh rằng tứ giác nội tiếp đường tròn
c) Gọi là tiếp tuyến chung của và với và . cắt tại . Chứng minh rằng .

Lời giải
a) Dễ thấy thẳng hàng và 
 là ba đường cao của nên chúng đồng quy tại 
b) Dễ thấy cùng thuộc một đường tròn đường kính 
c) Ta có 
 (1)
Tương tự ta có: (2)
Từ (1)(2) (đpcm).

Bài 5:
Cho hai đường tròn và (O’) cắt nhau tại và . Vẽ , thứ tự là đường kính của hai đường tròn và (O’)
a) Chứng minh ba điểm , , thẳng hàng
b) Đường thẳng cắt đường tròn tại đường thẳng cắt đường tròn tại . Chứng minh điểm cùng nằm trên một đường tròn
c) Một đường thẳng thay đổi luôn đi qua cắt và (O’) thứ tự tại và . Xác định vị trí của để đạt giá trị lớn nhất.

Lời giải
a) Do thẳng hàng
b) Do cùng thuộc một đường tròn
c) Gọi là trung điểm của . là điểm cố định
Gọi là trung điểm của 
Do , cùng vuông góc với nên là hình thang vuông
Nên 
Nhưng 
Vậy đạt giá trị lớn nhất khi đường thẳng vuông góc với .

Bài 6:
Cho tam giác vuông (vuông tại cố định nội tiếp đường tròn . là một điểm di động trên cung tròn khồng chứa . là giao điểm của và . Chứng minh giao điểm (khác của đường tròn với đường tròn ngoại tiếp tam giác là cố định.

Lời giải
Gọi là giao điểm thứ hai của giao điểm giữa đường thẳng qua vuông góc với và đường tròn 
Rõ ràng là đường trung trực của đoạn và là điểm cố định
Ta có: (quan hệ vuông góc ở tâm và góc nội tiếp)
Mà nên dễ thấy 
Từ (1)(2) ta suy ra . Vậy nên điểm cùng thuộc một đường tròn.
Tức là đường tròn và đường tròn ngoại tiếp tam giác cùng đi qua điểm cố định.

Bài 7:
Cho tam giác đều nội tiếp đường tròn . Gọi là đường tròn tiếp xúc trong với đường tròn và tiếp xúc với hai cạnh , theo thứ tự tại và 
a) Chứng minh rằng ba điểm , , thẳng hàng
b) Tính bán kính của đường tròn theo 

Lời giải
a) Gọi là tiếp điểm của hai đường tròn. Ta có thẳng hàng
Kẻ tiếp tuyến chung tại cắt , ở , 
Ta có đều là giao điểm của các đường trung trực của tam giác 
Suy ra , lần lượt là trung điểm của , 
Ta lại có là trung điểm của nên , , thẳng hàng
b) Vì đều nên O’ là trọng tâm của tam giác
Do đó .

Bài 8:
Cho đường tròn đường kính , đường tròn (O’) tiếp xúc trong với đường tròn tại . Các dây , của đường tròn tiếp xúc với đường tròn (O’) theo thứ tự tại , . Gọi là giao điểm của và . Chứng minh là tâm của đường tròn nội tiếp tam giác .


Lời giải
Do tính đối xứng nên 
Ta có (cùng bằng ) nên (tính chất của tia phân giác)
Suy ra lại có 
Điểm là giao điểm của các đường phân giác của các góc và của tam giác nên là tâm đường tròn nội tiếp tam giác đó.

Bài 9:
Cho đường tròn tâm đường kính . Gọi là bán kính vuông góc với , là tiếp tuyến với nửa đường tròn tại . Gọi là đường tròn tiếp xúc vưới nửa đường tròn tâm và tiếp xúc với đường kính . Chứng minh rằng điểm cách đều đường thẳng và điểm .


Lời giải
Giả sử đường tròn tiếp xúc với tại và tiếp xúc với tại 
Khi đó ba điểm thẳng hàng
Tiếp tuyến của đường tròn tại cắt ở và cắt ở 
Ta có 
Suy ra tứ giác là hình chữ nhật 
Do đó và 
Mặt kkác 
Vậy cách đều và .

Bài 10:
Cho nửa đường tròn đường kính , là một điểm trên nửa đường tròn sao cho , là hình chiếu của trên . Gọi là trung điểm của , đường tròn cắt nửa đường tròn tại và cắt cạnh , theo thứ tự tại và , đường thẳng cắt tại . Chứng minh rằng là hình chữ nhật, từ đó suy ra thẳng hàng.

Lời giải
 là đường kính của đường tròn 
Vậy tứ giác là hình chữ nhật.
 là trung điểm của , tức là thẳng hàng 
Gọi là trung điểm của , ta có 
Vì đường tròn và đường tròn cắt nhau tại điểm và nên 
Theo giả thiết là trực tâm 
Từ (2)(3) suy ra thẳng hàng 
Từ (1)(4) suy ra thẳng hàng (đpcm).

Bài 11:
Cho hai đường tròn và tiếp xúc ngoài tại và hai điểm lần lượt trên và sao cho . Chứng minh rằng 

Lời giải
Gợi : Giả thiết ta nghĩ đến điểm là giao điểm của và đường tròn 
Ta lần lượt có thẳng hàng
, từ đó sẽ suy ra kết quả 
Điểm phụ thuộc là “chìa khóa” để giải toán.
Hướng dẫn giải:
Vẽ đường kính của đường tròn 
Ta có (góc nội tiếp chắn nửa đường tròn)
Vì thẳng hàng
Xét có cân tại 
Chứng minh tương tự ta có , mà (đối đỉnh)
Nên so le trong
Vậy .

Bài 12:
Cho hai đường tròn và tiếp xúc ngoài tại . Kẻ tiếp tuyến chung ngoài 
a) Tính 
b) Tính 
c) Gọi là giao điểm của với đường tròn tâm . Chứng minh rằng ba điểm thẳng hàng
d) Tính 

Lời giải
a) Kẻ tiếp tuyến chung trong tại , cắt tại 
Ta có 
b) Ta có (tia phân giác của hai góc kề bù) nên 
Tam giác vuông tại , đường cao nên 
c) Ta có 
 vuông tại nội tiếp đường tròn nên là đường kính 
d) Tam giác vuông tại nên: 
Tương tự tính được .

Bài 13:
Cho hai đường tròn và tiếp xúc ngoài tại , góc vuông thay đổi luôn đi qua , cắt đường tròn và tại và . Gọi là hình chiếu của trên . Xác định vị trí của để có độ dài lớn nhất.

Lời giải
Kẻ đường kính , theo giả thiết thẳng hàng
Từ kẻ 
Do đó lớn nhất khi , đẳng thức xảy ra khi là tipp tuyến chung của hai đường tròn và .

Bài 14:
Cho hai đường tròn và tiếp xúc ngoài, tiếp tuyến chung ngoài ( thuộc , thuộc (O’)). Đường tròn tiếp xúc với và hai đường tròn và (O’). Chứng minh rằng , từ đó suy ra .

Lời giải
Giả sử từ O’ kẻ đường thẳng song song với cắt tại 
Suy ra tứ giác ABO’D là hình chữ nhật 
Ta có 
Theo định lí pitago ta có 
Theo giả thiết, đường tròn tiếp xúc với và hai đường tròn và (O’), gọi là tiếp điểm của đường tròn với 
Tương tự chứng minh trên suy ra và 
, chia cả hai vế cho được .

Bài 6: Vẽ đường phụ
*) Các đường hay vẽ thêm thường là dây cung của đường tròn, đường kính của đường tròn, tiếp tuyến của đường tròn, tiếp tuyến chung của hai đường tròn tiếp xúc nhau.
Bài 1: Vẽ đường phụ là dây cung
Cho đường tròn tâm , dây ( và điểm nằm trong góc ). Gọi là trung điểm của . Khoảng cách từ đến bằng 
a) Chứng minh rằng cân tại 
b) Tính bán kính của đường tròn.

Lời giải
a) Từ hạ 
Chứng minh là trung điểm của 
Vì , mà là trung điểm của 
Suy ra là trung điểm của 
Xét vuông tại 
 là trung điểm của 
b) thẳng hàng vì cùng thuộc trung trực của 
.

Bài 2: Vẽ đường phụ là đường kính
Cho hai đường tròn và với tiếp xúc ngoài tại và hai điểm lần lượt trên và (O’) sao cho . Chứng minh rằng .

Lời giải
Kẻ đường kính 
Vậy , mà nằm ở vị trí so le trong .

Bài 3: Vẽ thêm tiếp tuyến của đường tròn
Cho nửa đường tròn đường kính , bán kính vuông góc với . là điểm trên nửa đường tròn ( khác , . Tiếp tuyến của nửa đường tròn tại cắt và cắt tiếp tuyến tại của nửa đường tròn tâm lần lượt tại và . cắt tại . Chứng minh rằng .

Lời giải
Gọi . là giao điểm của tiếp tuyến với tiếp tuyến tại 
Theo tính chất tiếp tuyến cắt nhau 
Theo tính chất hai tiếp tuyến cắt nhau lần lượt là phân giác của và , mà hai góc này kề bù 
Áp dụng hệ thức lượng trong tam giác vuông vuông tại , có:
Ta đi chứng minh 
Xét có , là trung điểm của là trung điểm của 
Suy ra .

Bài 4:
Cho đường tròn tâm , đường thẳng cố định đi qua . Lấy điểm bất kì trên đường thẳng và ở ngoài đường tròn . Vẽ đường tròn tâm bán kính . Vẽ tiếp tuyến chung của hai đường tròn ( nằm trên , nằm trên ). Chứng tỏ rằng khi di động trên đường thẳng và ở ngoài đường tròn thì di động trên một đường cố định.

Lời giải
Từ kẻ tiếp tuyến với đường tròn , là tiếp điểm
Ta đi chứng minh đường thẳng là cố định, suy ra chứng minh cố định
Nhận xét: thuộc đường tròn 
Để chứng minh cố định ta chứng minh ba điểm thẳng hàng 
Ta có 
Vậy nằm trên hai tia đối nhau và 

Bài 5: Vẽ tiếp tuyến chung của hai đường tròn tiếp xúc
Cho hai đường tròn và cắt nhau tại và . Vẽ hình bình hành . Chứng minh rằng 

Lời giải
Theo tính chất hai đường tròn cắt nhau tại và 
 tại trung điểm của 
Theo giả thiết là hình bình hành nên cắt tại là trung điểm của 
Xét , có là đường trung bình 

Bài 6: Vẽ tiếp tuyến chung của hai đường tròn tiếp xúc
Cho hai đường tròn và có bán kính và tiếp xúc ngoài nhau. Một tiếp tuyến chung ngoài của và với các tiếp điểm lần lượt là và . Tính bán kính của đường tròn tiếp xúc với , và 

Lời giải
Kẻ tiếp tuyến chung tại cắt tại 
Theo tính chất tiếp tuyến lần lượt là phân giác của hai góc kề bù 
Xét hệ thức lượng trong tam giác 
GỌi bán kính , giả sử tiếp xúc với tại 
Tương tự ta có 
Vậy .

Bài 7: 
Cho đường tròn tâm bán kính . Điểm thuộc bán kính và cách là . Qua kẻ dây có độ dà ... : 
: đường kính
: Bán kính
2. Diện tích của hình tròn: 
3. Lấy hai điểm và có 
- Độ lớn của cung có góc ở tâm bằng 
- Diện tích hình quạt có góc ở tâm bằng 
- Diện tích của hình viên phân: Là hình giới hạn bởi dây cung và cung , có góc ở tâm bằng 
- Diện tích của hình vành khăn (hình xuyến)
B. Bài tập vận dụng
Bài 1:
Cho ba đường tròn tiếp xúc ngoài nhau từng đôi một. Gọi là tiếp điểm của và , là tiếp điểm của và . Tính độ dài cung nhỏ của .
Lời giải
Ta có 
Nhận thấy 
 vuông tại 
Từ đó .

Bài 2:
Cho đường tròn và hai đường kính , vuông góc với nhau. Vẽ cung tròn tâm , bán kính . Tính diện tích phần hình lưỡi liềm tạo bởi cung của đường tròn tâm và cung (có chứa ) của đương tròn 

Lời giải
Dễ thấy 
Diện tích hình quạt của đường tròn là: 
Diện tích là: 
DIện tích hình viên phân giới hạn bởi và dây của là:
Vậy diện tích hình lưỡi liềm là: .

Bài 3:
Cho , đường thẳng tiếp xúc với tại . Từ điểm trên đường tròn vẽ . Đường cao của cắt tại 
a) Chứng minh rằng 
b) Chứng minh rằng 
c) Biết rằng sđ. Tính diện tích hình giới hạn bởi dây cung và cung nhỏ 

Lời giải
a) Ta có (góc cso cạnh tương ứng vuông góc)
b) Ta có 
 cân tại là phân giác 
c) 
Diện tích hình quạt giới hạn bởi và cung , dây cung 
Tính được 
.

Bài 4:
Cho nửa đường tròn tâm , đường kính . Một điểm thuộc nửa đường tròn sao cho . Vẽ hai nửa đường tròn đường kính và ở phía ngoài . Chứng minh rằng , trong đó là diện tichs hình trăng khuyết như hình vẽ.


Lời giải
Nửa hình tròn đường kính có diện tích là 
Từ đó, ta có 
Lại có 
 (đp\text{cm}).

Bài 5:
Cho và tiếp xúc ngoià nhau tại . Vẽ các tiếp tuyến chung ngoài với và 
a) Chứng minh rằng 
b) Tính độ dài 
c) Tính diện tích hình giới hạn bởi đoạn thẳng , cung nhỏ của , cung nhỏ của 

Lời giải
a) Hạ 
Trong tam giác vuông có (đp\text{cm})
b) mà ()
c) 
 ().

Bài 6:
Cho điểm thuộc đoạn thẳng sao cho . Vẽ về phía của các nửa đường tròn có đường kính và có tâm theo thứ tự là . Đường thẳng vuông góc với tại cắt tại . Gọi theo thứ tự là giao điểm của với và 
a) Chứng minh rằng 
b) Chứng minh rằng là tiếp tuyến chung của và 
c) Tính độ dài đoạn thẳng 
d) Tính diện tích hình giới hạn bởi nửa đường tròn
e) Giả sử di động trên . Tìm vị trí của để diện tích hình thang đạt giá trị lớn nhất.

Lời giải
a) Dễ thấy là hình chữ nhật (tứ giác có ba góc vuông)
b) Ta có 
Chứng minh tương tự ta có: 
c) , mà 
d) 
 lớn nhất thì lớn nhất, mà 
Dấu “=” xảy ra .
Bài 7:
Từ điểm nằm ngoài , kẻ tiếp tuyến với . Từ điểm trên cung nhỏ . Kẻ một tiếp tuyến với cắt lần lượt tại và 
a) Chứng minh rằng khi chuyển động trên cung nhỏ thì chu vi có giá trị không đổi
b) Cho và bán kính của là . Tính độ dài và diện tích phần mặt phẳng giới hạn bởi tiếp tuyến và cung nhỏ .

Lời giải
a) Ta có 
b) Theo giả thiết 
Ta có 
 ().

Bài 8:
Cho đường tròn tâm , đường kính và có bán kính . Gọi là trung điểm của . Vẽ dây tại . Lấy điểm 
Trên đoạn . cắt đường tròn tại điểm thứ hai là 
a) Chứng minh rằng 
b) Tính độ dài cùng nhỏ khi 
(tính chính xác đến chữ số thập phân sau dấu phẩy).

Lời giải
a) Dễ thấy sđ sđ
 (gg)
b) Nhắc lại 
tan
 (\text{cm}).

BÀI TẬP TƯƠNG TỰ DẠNG TOÁN
Bài 1:
Cho đường tròn , dây cố định () và điểm di động trên cung lớn sao cho tam giác có ba góc nhọn. Các đường cao và của tam giác cắt nhau ở .
a) Chứng minh rằng tứ giác nội tiếp
b) Giải sử , hãy tính khoảng cách từ tâm đến cạnh theo 
c) Chứng minh rằng đường thẳng kẻ qua và vuông góc với luôn đi qua một điểm cố định.

Lời giải
b) Kẻ 
c) Ta có (cùng phụ với )
 (góc nội tiếp chắn cung 
Từ đó 
Vậy đường thẳng qua vuông góc với luôn đi qua tâm cố định.

Bài 2:
Cho cân tại , là tâm đường tròn nội tiếp, là tâm đường tròn bàng tiếp góc , là trung điểm của 
a) Chứng minh điểm cùng thuộc một đường tròn tâm 
b) Chứng minh là tiếp tuyến của đường tròn 
c) Tính bán kính của đường tròn , biết 


Lời giải
b) Chứng minh được 
Vậy là tiếp tuyến của 
c) Gọi lần lượt là tiếp điểm của 
Với cạnh . Gọi là tiếp điểm của với đường thẳng 
Ta có 
Như vậy, tính được 
Đặt là bán kính của , là bán kính của 
Trong tam giác vuông có: 
Tương tự, trong tam giác vuông ta có 
Vậy bán kính của là 

Bài 3:
Cho hai đường tròn và tiếp xúc ngoài. Vẽ tiếp tuyến chung ngoài với thứ tự là các tiếp điểm thuộc đường tròn và (O’)
a) Chứng minh 
b) Tính theo 
c) Gọi là giao điểm của đường thẳng và đường tròn (), vẽ tiếp tuyến với đường tròn (). Tính theo và 

Lời giải
a) Kéo dài cắt tại điểm thứ hai là 
Vì 
Mà 
Không mất tính tổng quát, giả sử . Khi đó ănmf giữa O’ và và 
Từ đó 
c) Dễ thấy thẳng hàng
Trong hình thang vuông ta có:
Trong tam giác vuông ta có: .

Bài 4:
Cho nửa đường tròn với đường kính . Dây song song với ( thuộc cung . Cho biết chu vi hình thang bằng . Tính độ dài các cạnh của hình thang 


Lời giải
Dễ thấy là hình thang cân
Hạ vuông góc với 
Đặt 
Từ 
Ta có 
Tam giác vuông tại nên 
Vậy .

Bài 8: Luyện tập
Bài 1: Chuyên Bình Phước, năm học 2018
Cho đường tròn và điểm nằm bên ngoài , kẻ các tiếp tuyến và cát tuyến không đi qua ( nằm giữa và )
a) Chứng minh rằng tứ giác nội tiếp
b) 
c) Gọi là giao điểm của và . Chứng minh rằng là tia phân giác của .

Lời giải
a) Dễ thấy cùng thuộc đường tròn đường kính 
Vậy tứ giác nội tiếp
b) Ta có (gg)
const
c) Giả sử tia nằm giữa và 
Ta có: (gg) 
 tứ giác là tứ giác nội tiếp 
Mà (phụ với hai góc bằng nhau)
 là phân giác của .

Bài 2: Chuyên Lê Hồng Phong, năm học 2015
Cho vuông tại , đường cao . Đường tròn tâm đường kính cắt cạnh lần lượt tại và . Gọi là trung điểm của . Gọi là giao điểm của và 
1) Chứng minh rằng:
a) 
b) Tứ giác nội tiếp
2) Chứng minh rằng:
a) 
b) 
3) Gọi là giao điểm của và , là giao điểm thứ hai của và . Chứng minh rằng .

Lời giải
1) a) Dễ thấy 
b) Từ cùng thuộc một đường tròn
Hoặc nội tiếp.
2) a) Ta có ( cân tại 
, mà (phụ )
 (gg)
b) , mà 
3) Theo 1b) tứ giác nội tiếp (*)
Lại có tứ giác nội tiếp (**)
Từ (*) và (**) cùng thuộc một đường tròn
Mà thuộc đường tròn đường kính .

Bài 3: Chuyên Bà Rịa Vũng Tàu, năm học 2018
Cho đường tròn và là một dây cung không đi qua . Gọi là trung điểm của . Trên tia đối của tia lấy điểm khác . Vẽ các tiếp tuyến với và tiếp điểm thuộc cung nhỏ 
a) Chứng minh rằng nội tiếp đường tròn
b) Chứng minh rằng 
c) Đường thẳng cắt cung nhỏ của tại . Gọi là giao điểm của và . Chứng minh rằng cân tại .
d) Đường thẳng cắt đường thẳng tại . Chứng minh rằng .

Lời giải
a) Ta có đp\text{cm}
b) 
c) Ta có sđ (góc tạo bởi tia tiếp tuyến và dây cung)
Mà 
 cân tại (đp\text{cm}).

Bài 4:
Cho có ba góc nhọn. Kẻ tiếp tuyến và . Trên nửa đường tròn đường kính không chứa và lấy điểm bất kỳ. Gọi lần lượt là hình chiếu vuông góc của trên . Tìm của tổng sau 

Lời giải
Lấy trên nửa đường tròn đường kính có chứa sao cho 
Gọi (gg)
Tương tự ta có: (gg)
Từ (1)(2) đạt khi nằm chính giữa cung .

Bài 5: Chuyên TPHCM, năm học 2015
Cho tam giác có ba góc nhọn nội tiếp đường tròn . Gọi là trung điểm của và là điểm đối xứng của qua . Đường thẳng qua vuông góc với cắt đường thẳng qua vuông góc với tại . Kẻ đường kính . Chứng minh rằng:
a) 
b) đi qua trung điểm của đường cao của tam giác 

Lời giải
a) Ta có (cùng phụ với )
 lần lượt là điểm đối xứng của qua nên 
Ta lại có và 
Từ (1)(2) suy ta 
b) Gọi là giao điểm của và 
Dễ thấy 
Vậy để chứng minh đi qua trung điểm của , ta sẽ chứng minh là trung điểm của 
Thật vậy, ta có theo phần a) thì 
Mà (chắn cung 
 là trung điểm của nên là trung điểm của .

Bài 6: Chuyên Khánh Hòa, năm học 2015
Cho tam giác vuông tại . Hai đường tròn và cắt nhau tại điểm thứ hai là . Vẽ đường thẳng bát kì qua cắt đường tròn tại và cắt đường tròn tại ( nằm giữa và . Tiếp tuyến tại của đường tròn và tiếp tuyến tại của đường tròn cắt nhau tại .
a) Chứng minh là tia phân giác của 
b) Gọi là giao điểm của và . Chứng minh rằng 
c) Chứng minh bốn điểm cùng thuộc một đường tròn
d) Chứng minh rằng số đo góc không phụ thuộc vào vị trí của đường thẳng .

Lời giải
c) Ta có (hệ quả tính chất góc tạo bởi tia tiếp tuyến và dây cung)
 (hệ quả tính chất góc tạo bởi tia tiếp tuyến và dây cung)
Suy ra 
Trong tam giác có 
Hay nội tiếp
d) Trong tam giác có 
mà 
Ta lại có (góc ở tâm và góc nội tiếp chắn một cung)
Mà vuông tại nên (không đổi)
Vậy số đo góc không phụ thuộc vào đường thẳng .

Bài 7: Chuyên Hùng Vương, năm học 2015
Cho hình vuông tâm , là điểm di động trên cạnh . Trên cạnh lấy điểm sao cho , trên cạnh lấy điểm sao cho 
a) Chứng minh rằng đường thẳng là phân giác trong của góc , đường thẳng là phân giác trong của góc . Từ đó suy ra ba điểm thẳng hàng
b) Gọi là chân đường vuông góc kẻ từ tới đường thẳng . Chứng minh bốn điểm cùng nằm trên một đường tròn.
c) Chứng minh rằng khi điểm di động trên cạnh thì đường thẳng luôn đi qua một điểm cố định.

Lời giải
a) Dễ thấy 
Vậy là phân giác trong của góc 
Chứng minh tương tự, ta có là phân giác trong của góc 
Từ đó chứng minh được thẳng hàng
b) Tứ giác nội tiếp đường tròn đường kính nên 
Tứ giác nội tiếp đường tròn đường kính nên 
Tứ giác nội tiếp đường tròn đường kính nên 
Suy ra 
Ta thấy và cùng nhìn dưới một góc vuông nên bốn điểm cùng nằm trên một đường kính 
c) Đường thẳng cắt đường tròn đường kính tại điểm thứ hai 
Ta có là điểm chính giữa cung (không chứa ) của đường tròn đường kính 
Hoặc, dễ thấy là đường kính của đường tròn đường kính . cố định nên cố định.

Bài 8:
Cho đường tròn và dây cung cố định. Điểm di động trên cung lớn sao cho tam giác nhọn. Gọi là điểm đối xứng với qua và là điểm đối xứng với qua . Các đường tròn ngoại tiếp các tam giác và cắt nhau tại ( không trùng . Gọi là giao điểm của và 
a) Chứng minh là phân giác trong góc và tứ giác nội tiếp
b) Xác định vị trí điểm để diện tích tứ giác lớn nhất, tính diện tích lớn nhất của tứ giác đó theo 
c) Chứng minh luôn đi qua điểm cố định.

Lời giải
a) Ta có (vì cùng chắn cung của đường tròn ngoại tiếp tam giác AEB)
Mà (tính đối xứng) suy ra .
 (vì cùng chắn cung của đường tròn ngoại tiếp tam giác AFC)
 (tính chất đối xứng) suy ra 
Mặt khác (cùng phụ với ) 
Từ (1)(2)(3) suy ra hay là phân giác trong của 
Gọi lần lượt là các giao điểm của và và với 
Ta có nên 
Trong tam giác vuông có 
Tứ giác có: (đối đỉnh)
Ta có (chứng minh phần a)
Mà 
Nên tứ giácBHCK nội tiếp
b) Gọi là đường tròn đi qua bốn điểm 
Ta có dây cung , nên bán kính đường tròn bán kính của đường tròn 
Gọi là giao điểm của và thì vuông góc với .
Kẻ vuông góc với ( thuộc )
Gọi là giao điểm của và 
Ta có 
Ta có là dây cung của đường tròn (không đổi)
Nên lớn nhất khi 
Giá trị lớn nhất 
Khi là đường kính của đường tròn thì trùng nhau suy ra là trung điểm của nên cân tại . Khi đó là điểm chính giữa cung lớn 
c) Ta có nên tứ giác nội tiếp đường tròn.
Ta có suy ra hay là phân giác góc 
Theo phần ta có là phân giác góc nên thẳng hàng hay đi qua cố định.