Đề cương thi vào lớp 10 môn Toán

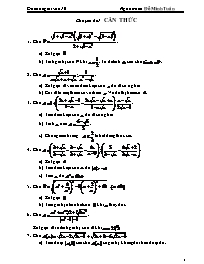
Chuyên đề 1: CĂN THỨC
Cho .
Rút gọn .
Tính giá trị của khi . Từ đó tính sao cho .
Cho .
Rút gọn và nêu điều kiện của để có nghĩa.
Coi là một hàm số với biến . Vẽ đồ thị hàm số .
Cho .
Tìm điều kiện của để có nghĩa.
Tính nếu .
Chứng minh rằng : là bất đẳng thức sai.
Cho .
Rút gọn .
Tìm điều kiện của để .
Tìm để .
Cho .
Rút gọn .
Tìm giá trị nhỏ nhất của khi thay đổi.
Cho .
Rút gọn rồi tính giá trị của khi .
Cho .
Tìm đoạn sao cho có giá trị không đổi trên đoạn đó.
Tìm sao cho .
Cho . Tính : .
Cho .
Tìm để .
Tìm để đạt giá trị nhỏ nhất. 
Cho . Tính .
Rút gọn các biểu thức sau : 
 .
Cho ,.
 Chứng minh : .
Chứng minh các biểu thức sau là một số vô tỷ : 
Cho .
 Chứng minh : là một số nguyên.
Rút gọn biểu thức : .
Chuyên đề 2: PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Giải các phương trình sau đây bằng cách đặt ẩn số phụ thích hợp :
.
.
.
.
.
.
.
.
.
.
.
.
.
Tìm các nghiệm nguyên hoặc của các phương trình và hệ phương trình dưới đây:
.
.
Giải các phương trình, hệ phương trình khác dưới đây:
.
.
.
.
Tìm nghiệm nguyên của phương trình : .
Phân tích biểu thức thành nhân tử. Từ đó giải hệ : 
Tìm các số nguyên thỏa mãn điều kiện : 
Tìm các số nguyên để là nghiệm của phương trình sau : 
 Giải phương trình : .
Cho phương trình : .
 Biết rằng phương trình đã cho có 4 nghiệm phân biệt . Chứng minh :
 .
Chuyên đề 3: BẤT ĐẲNG THỨC. GIÁ TRỊ MIN, MAX
Cho là độ dài 3 cạnh của tam giác. Chứng minh : 
 Khi nào có đẳng thức xảy ra ?
Giả sử . Chứng minh : .
Cho và . Chứng minh : .
Cho 3 số phân biệt . Chứng minh rằng có ít nhất một trong 3 số sau đây là số dương : 
Chứng minh rằng : nếu thỏa mãn : thì .
Chứng minh : .
Chứng minh rằng : nếu là các số đôi một khác nhau và thì 
Chứng min rằng : nếu là số tự nhiên.
Chứng minh rằng nếu thì : .
Chứng minh rằng : với . Từ đó suy ra :
 ()
Cho hai số thỏa mãn : và . Chứng minh : . 
Cho có các cạnh thỏa mãn : . Chứng minh : 
Ba số dương . Chứng minh rằng 3 số không đồng thời lớn hơn 1.
Ba số dương thỏa mãn . Chứng minh :
Cho và . Tìm giá trị nhỏ nhất của biểu thức : 
Tìm giá trị lớn nhất nhỏ nhất của hàm số : .
Cho (). Tìm để đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của : .
Các số thỏa mãn điều kiện : 
Tìm giá trị lớn nhất và giá trị nhỏ nhất của .
Tìm cặp số thỏa mãn đẳng thức : sao cho đạt giá trị lớn nhất.
Cho .
Rút gọn biểu thức .
Tìm để có giá trị nhỏ nhất.
Tìm giá trị lớn nhất của hàm số : .
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số :
.
Với giá trị nào của thì : đạt giá trị nhỏ nhất ? Tìm giá trị nhỏ nhất đó.
Tìm giá trị lớn nhất, nhỏ nhất biết .
Cho các số dương thỏa mãn điều kiện . Chứng minh :
 .
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức : .
Tìm giá trị lớn nhất của hàm số : .
Chứng minh rằng : .
Chứng minh rằng : .
Chuyên đề 4: ĐA THỨC VÀ NHỮNG VẤN ĐỀ LIÊN QUAN
Cho . Với giá trị nào của thì với mọi giá trị của trong tập xác định của chúng.
Cho .
Tìm để đẳng thức trên đúng với mọi .
Cho với .
Phân tích thành nhân tử.
Tìm để .
Chứng minh rằng : chia hết cho 30.
Chứng minh rằng : nếu là những số nguyên thỏa mãn điều kiện chia hết cho 3 thì cả đều chia hết cho 3.
Tìm giá trị của để đa thức chia hết cho đa thức .
Cho đa thức với .
Phân tích thành nhân tử.
Chứng minh rằng đa thức chia hết cho 24
Cho . Chứng minh rằng khi nguyên thì chia hết cho .
Tìm tất cả các số nguyên để chia hết cho .
Một đa thức chia cho thì dư 5, chia cho dư 7. Tính phần dư của phép chia đa thức đó cho .
Cho và . Với giá trị nào của thì chia hết cho .
Cho biết tổng các số nguyên chia hết cho 3. Chứng minh rằng : 
 cũng chia hết cho 3.
Chứng minh rằng : luôn chia hết cho 19, với mọi số tự nhiên .
Tìm các số nguyên để biểu thức phân tích được thành 2 đa thức bậc nhất với hệ số nguyên.
Tìm để phương trình sau có nghiệm là mọi số thực .
Phân tích đa thức sau thành nhân tử : .
Cho đa thức .
Phân thức đa thức thành nhân tử.
Tìm để triệt tiêu.
Chứng minh rằng chia hết cho 120.
Tìm đa thức biết rằng khi chia cho dư ; khi chia cho dư 3, khi chia cho được thương là và còn dư.
Cho . Chứng minh rằng : khi là số nguyên thì cũng nhận giá trị là số nguyên.
Chuyên đề 5: HÀM SỐ VÀ ĐỒ THỊ
Cho hai hàm số . Vẽ đồ thị rồi tìm giá trị của để đồ thị hàm số chỉ có một điểm chung với đồ thị . Trong trường hợp hai đồ thị cắt nhau tại 2 điểm . Tìm tọa độ trung điểm của đoạn thẳng .
Cho hình chữ nhật có độ dài hai cạnh là nghiệm của phương trình : 
Tìm để hình chữ nhật trên tồn tại.
Gọi theo thứ tự là chu vi và diện tích của hình chữ nhật đó. Vẽ đồ thị biểu diễn sự biến thiên của theo trên cùng một$hệ tọa độ. Hai đồ thị của có cắt nhau không ? 
Cho hệ tọa độ Oxy và 2 điểm 
Viết phương trình ba đường thẳng chứa 3 cạnh . Chỉ rõ giới hạn của để trên đường thẳng đó ta được 3 đoạn thẳng là 3 cạnh của .
Viết phương trình đường Parabol có đỉnh ở và đi qua . Chứng minh Parabol đó đi qua .
Vẽ các đoạn thẳng và Parabol trên cùng một hệ trục tọa độ.
Cho hệ tọa độ Oxy và 3 điểm .
Lập phương trình đường thẳng .
Chứng minh rằng 3 đường thẳng và là những đường thẳng đồng quy.
Chứng minh rằng : là 3 điểm thẳng hàng.
Vẽ đồ thị hàm số .
Cho hàm số 
Vẽ đồ thị hàm số đã cho.
Viết phương trình đường thẳng đi qua điểm tiếp xúc với phần đường Parabol đã vẽ ở trên.
Cho hàm số .
Tìm để đồ thị hàm số cắt trục hoành tại 2 điểm thỏa mãn : và .
Tìm để đồ thị hàm số cắt trục hoành tại 2 điểm đối nhau qua gốc tọa độ. Tìm 2 điểm đó.
Vẽ đồ thị hàm số .
Vẽ đồ thị hàm số . Từ đó hãy suy ra đồ thị hàm số .
Cho hàm số : .
Tìm biết đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 1, cắt trục hoành tại điểm có hoành độ bằng 1, và đi qua điểm .
Tìm giao điểm còn lại của đồ thị hàm số với trục hoành.
Chứng minh rằng đồ thị hàm số tiếp xúc với đường thẳng .
Cho hàm số : .
Tìm để đồ thị hàm số song song với đường thẳng .
Tìm để đồ thị hàm số đi qua điểm .
Tìm để đồ thị hàm số đã cho và các đường thẳng đồng qui tại một điểm.
Cho hàm số . Chứng minh rằng hàm số đồng biến trên khoảng .
Lập phương trình đường thẳng đi qua 2 điểm và . Tìm để đường thẳng cắt đường thẳng tại một điểm trên trục tung.
Vẽ đồ thị hàm số : . Từ đó giải phương trình .
Chứng minh các đường thẳng có phương trình : luôn đi qua một điểm cố định với mọi giá trị của .
Cho parabol và đường thẳng 
Vẽ parabol . Tìm để tiếp xúc với .
Chứng minh rằng luôn đi qua một điểm cố định.
Cho hàm số . Chứng minh đồ thị hàm số trên luôn đi qua một điểm cố định với mọi giá trị của . Tìm để đồ thị trên là một parabol. Tìm các điểm trên mặt phẳng tọa độ mà không có Parabol nào nói trên đi qua.
Trong mặt phẳng tọa độ Oxy cho . Biết phương trình đường thẳng là ; Phương trình đường thẳng và trung điểm cạnh là . Lập phương trình đường thẳng .
Cho parabol trong hệ tọa độ Oxy. Tìm để đường thẳng cắt tại 2 điểm phân biệt sao cho .
Tìm miền xác định của hàm số : .
Trong mặt phẳng tọa độ Oxy cho Parabol và điểm và điểm với là tham số.
Vẽ parabol đã cho.
Viết phương trình đường thẳng đi qua 2 điểm . Chứng minh rằng luôn cắt parabol đã cho tại 2 điểm phân biệt với độ dài .
Chuyên đề 6: GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
Bài toán chuyển động 
Hai bến sông cách nhau 126 km. Một tàu thủy khởi hành từ xuôi dòng về . Cùng lúc đó có một đám bèo trôi tự do cùng chiều với tàu. Khi tàu về đến liền quay trở lại ngay và khi tàu về đến tính ra hết 16 giờ. Trên đường trở về , khi còn cách 28 km thì gặp lại đám bèo nói trên. Tính vận tốc riêng của tàu thuỷ và vận tốc của dòng nước chảy.
Lúc 9 giờ sáng một chiếc bè trôi tự do từ đến dọc theo bờ sông. Cùng lúc đó một chiếc thuyền khởi hành từ đến và sau 5 giờ thì gặp chiếc bè. Khi về đến , thuyền quay lại ngay và về tới cùng một lúc với chiếc bè. Hỏi thuyền và bè có kịp đến vào lúc 21 giờ ngày hôm đó hay không ?
Hai người đi bộ cùng khởi hành từ để đi đến và ( nằm giữa ). Người thứ nhất đi đến , người thứ 2 đi đến . Sau khi đến nơi cả hai quay lại ngay và họ gặp nhau ở trung điểm đoạn . Nếu ngược lại, người thứ nhất đến và người thứ 2 đến thì người thứ nhất sau khi đến quay lại ngay và đuổi kịp người thứ 2 tại . Tính khoảng cách từ đến và tỷ số vận tốc của 2 người biết rằng đoạn dài 2 km.
Một người đi từ đến rồi quay lại ngay mất tất cả 3 giờ 41 phút. Đoạn đường dài 9 km gồm một đoạn lên dốc, tiếp đó là một đoạn đường bằng, cuối cùng là một đoạn xuống dốc. Hỏi đoạn đường dài bằng bao nhiêu km, nếu biết vận tốc của người xuống dốc là 4 km/giờ, lúc đi đoạn đường bằng là 5 km/giờ và xuống dốc là 6 km/giờ.
Hai xe ô tô cùng khởi hành một lúc từ đến . Xe thứ nhất trong số thời gian cần thiết để đi hết đoạn đường thì nửa thời gian đầu nó đi với vận tốc 50 km/h; nửa thời gian còn lại đi với vận tốc 40 km/h. Xe thứ 2 trong nửa đoạn đường đầu nó đi với vận tốc vận tốc 40 km/h; nửa đoạn đường sau nó đi với vận tốc 50 km/h. Hỏi 2 xe đó có đi cùng về đến một lúc không ?
Trên tuyến đường có 2 người cùng khởi hành từ 2 địa điểm và . Người ở đi với vận tốc 20 km/h. Người ở đi với vận tốc 40 km/h. Người ở địa điểm khởi hành sau một giờ và đi với vận tốc 48 km/h. Biết dài 22 km còn dài 42 km. Hỏi sau bao lâu người đi từ vị trí sẽ cách đều người đi từ vị trí .
Bài toán công việc
Một bể đựng nước có 2 vòi : vòi đưa nước vào và vòi tháo nước ra. Vòi từ khi nước cạn tới khi nước đầy (có đóng vòi ) lâu hơn 2 giờ so với vòi tháo nước tù khi bể đầy tới khi bể cạn (có đóng vòi ). Khi bể nước chứa 1/3 thể tích của nó nếu người ta mở cả 2 vòi thì sau 8 giờ bể cạn nước. Hỏi sau bao nhiêu giờ riêng vòi có thể chảy đầy bể ? Sau bao nhiêu giờ riêng vòi có thể tháo hết nước trong bể ?
Hai vòi nước cùng chảy thì sau 5 giờ 50 phút sẽ đầy bể. Nếu để hai vòi cùng chảy trong 5 giờ rồi khóa vòi thứ 2 thì phải trong 2 giờ nữa mới đầy bể. Tính xem nếu để mỗi vòi chảy một mình thì trong bao lâu sẽ đầy bể ?
Các bài toán khác
Để chở một số bao hàng bằng ôtô, người ta nhận thấy nếu mỗi xe chở 22 bao thì còn thừa một bao. Nếu bớt đi một ôtô thì có thể phân phối đều các bao hàng cho các ôtô còn lại. Hỏi lúc đầu có bao nhiêu ôtô và tất cả có bao nhiêu bao hàng. Biết rằng mỗi ôtô chỉ chở được không quá 32 bao hàng (giả thiết mỗi bao hàng có khối lượng như nhau)
Mỗi người dán tất cả tem của mình vào một quyển vở. Nếu dán 20 tem trên một tờ thì quyển vở không đủ để dán hết số tem. Còn nếu mỗi tờ dán 23 tem thì ít nhất một tờ trong quyển vở còn bị bỏ trống. Nếu giả sử cũng trên quyển vở đó mà trên một tờ dán 21 tem thì tổng số tem dán trên quyển vở đó với số tem thực có của người đó là 500 tem. Hỏi quyển vở đó có bao nhiêu tờ và số tem người đó có ?
Tìm một số gồm ba chữ số sao cho khi ta lấy chữ số hàng đơn vị đặt về bên trái của một số gồm hai chữ số còn lại, ta được một có ba chữ số lớn hơn số ban đầu 765 đơn vị.
Một trăm con trâu ăn một trăm bó cỏ. Trâu đứng mỗi con ăn năm bó, trâu nằm mỗi con ăn ba bó, trâu già 3 con ăn một bó. Tìm số trâu mỗi loại ?
Tìm một số có 2 chữ số biết rằng nếu đem số đó chia cho tổng các chữ số của nó thì được thương là 4 và dư là 3. Còn nếu đem số đó chia cho tích các chữ số của nó thì được thương là 3 và dư là 5.
Hai đội cờ thi đấu với nhau. Mỗi đấu thủ của đội này phải đấu một ván với mỗi đấu thủ của đội kia. Biết rằng tổng số ván cờ đã đấu bằng bình phương số đấu thủ của đội thứ nhất cộng với số đấu thủ của đội thứ hai. Hỏi mỗi đội có bao nhiêu đấu thủ ?
Hai đội bóng bàn của hai trường thi đấu giao hữu để chuẩn bị tranh giải toàn tỉnh. Biết rằng mỗi đấu thủ của đội trường phải lần lượt gặp các đối thủ của trường một lần và số trận đấu gấp 2 lần tổng số đấu thủ của 2 đội. Tìm số đấu thủ của mỗi trường.
Trong một cuộc gặp mặt học sinh giỏi có 35 bạn học sinh giỏi văn và toán tham dự. Các học sinh giỏi văn tính số người quen của mình là các bạn học sinh giỏi toán và nhận thấy rằng : bạn thứ nhất quen 6 bạn ; Bạn thứ 2 quen 7 bạn ; Bạn thứ 3 quen 8 bạn ; ... và cứ thế bạn cuối cùng quen tất cả các bạn học sinh giỏi toán. Tính số học sinh giỏi văn, giỏi toán. Biết rằng không có học sinh nào vừa giỏi văn vừa giỏi toán.
Trong một buổi liên hoan, một lớp khách mời 15 khách đến dự. Vì lớp đã có 40 học sinh nên phải kê thêm một dãy ghế nữa và mỗi dãy ghế phải ngồi thêm một nữa thì mới đủ chỗ ngồi. Biết rằng mỗi dãy ghế đều có số người ngồi như nhau và ngồi không quá năm người. Hỏi lớp học lúc đầu có bao nhiêu dãy ghế
Một đoàn gồm 50 học sinh qua sông cùng một lúc bằng 2 loại thuyền : Loại thứ nhất, mỗi thuyền chở được 5 em và loại thứ 2 chở được 7 em mỗi thuyền. Hỏi số thuyền mỗi loại?
Tìm một số gồm 2 chữ số, biết rằng tổng các bình phương hai chữ số bằng số đó cộng thêm tích hai chữ số. Nếu thêm 36 vào số đó thì được một số có hai chữ số mà các chữ số viết thứ tự ngược lại.
Chuyên đề 7: PHƯƠNG TRÌNH BẬC 2 - ĐỊNH LÝ VIÉT
Cho phương trình : .
Chứng minh : phương trình luôn có 2 nghiệm với mọi .
Chứng minh có một hệ thức liên hệ giữa 2 nghiệm số không phụ thuộc .
Tìm những giá trị nguyên của để biệt thức của phương trình sau là số chính phương : .
Tìm để phương trình có 4 nghiệm phân biệt sao cho khi biểu diễn 4 nghiệm đó lên trục số nó chắn trục số thành 3 đoạn bằng nhau.
Tìm để phương trình sau đây có 3 nghiệm phân biệt : 
Chứng minh rằng phương trình bậc hai : không thể có nghiệm hữu tỷ nếu đều là số lẻ.
Tìm để hai phương trình sau tương đương : 
 và 
Giả sử là các nghiệm của phương trình : 
 Chứng minh : . 
Chứng minh rằng nếu các hệ số phương trình sau luôn có nghiệm :
Chứng minh rằng nếu các hệ số của phương trình : thỏa mãn điều kiện : thì phương trình sẽ có nghiệm này gấp đôi nghiệm kia.
Chứng minh rằng nếu với là các số dương thì phương trình sau đây vô nghiệm : .
Chứng minh rằng : là nghiệm của phương trình : .
Tìm giá trị của tham số để 2 bất phương trình sau đây có đúng một nghiệm chung : .
Cho 2 phương trình . Chứng minh rằng nếu thì ít nhất có một trong 2 phương trình trên phải có nghiệm.
Cho phương trình có nghiệm là .
Tính theo các biểu thức sau : 
Cho . Tìm hệ thức liên hệ giữa không phụ thuộc vào .
Chứng minh rằng nếu phương trình có 2 nghiệm dương thì phương trình cũng có 2 nghiệm dương.
Với giá trị nào của thì hai phương trình sau có ít nhất một nghiệm chung :
 .
Cho hai phương trình : 
Tìm để 2 phương trình (1), (2) có cùng tập hợp nghiệm.
Tìm để phương trình có 2 nghiệm sao cho .
Cho hàm số , tìm để đồ thị hàm số cắt trục hoành tại 2 điểm có hoành độ thỏa mãn : .
Tìm các giá trị của sao cho 2 phương trình có nghiệm chung.
Cho phương trình : ( là tham số)
Tìm để phương trình trên có 2 nghiệm phân biệt . Khi đó tìm hệ thức liên hệ giữa không phụ thuộc vào . Tìm để phương trình trên có 2 nghiệm thỏa mãn hệ thức : .
Chuyên đề 8:
CÁC BÀI TOÁN HÌNH HỌC PHẲNG CÓ YẾU TỐ CHUYỂN ĐỘNG
Cho nửa đường trong đường kính ; là bán kính vuông góc với . Gọi là điểm di động trên đoạn (). Tia cắt đường tròn tại . Tiếp tuyến tại với đường tròn cắt đường thẳng tại .
Chứng minh cân.
Nêu cách dựng điểm để . Khi đó tính các góc của .
Nếu cách dựng điểm để . Khi đó tính .
Chứng minh tâm đường tròn ngoại tiếp nằm trên đường thẳng cố định.
Trên đường tròn lấy điểm cố định và điểm thay đổi. Đường vuông góc vẽ từ cắt đường tròn ở .
Chứng minh đường thẳng luôn đi qua một điểm cố định.
Gọi là đường cao vẽ từ của . Tìm tập hợp các điểm .
Dựng vuông có đỉnh cho trước trên đường tròn, là đường kính và chiều cao cho trước.
Gọi là trung điểm . Chứng minh đi qua một điểm cố định. Dựng có đỉnh cho trước trên đường tròn, cạnh là đường kính của đường tròn ấy và có trung tuyến cho trước.
Cho đường tròn tâm cố định. Một đường thẳng cố định cắt đường tròn tại ; là một điểm chuyển động trên (ở ngoài đoạn ). Từ kẻ 2 tiếp tuyến với đường tròn.
Chứng minh đường tròn luôn đi qua một điểm cố định .
Tìm tập hợp các tâm của đường tròn .
Tìm trên điểm sao cho đều.
Cho đường tròn tâm đường kính . Gọi là điểm thay đổi trên đường tròn. Khi , dựng đường tròn tâm tiếp xúc với tại . Từ vẽ 2 tiếp tuyến với đường tròn tâm vừa dựng.
Chứng minh nằm trên tiếp tuyến với đường tròn tâm tại .
Chứng minh không đổi, từ đó tính tích theo .
Giả sử ngoài , trên đường tròn còn có điểm cố định. Gọi là trung điểm của , kẻ vuông góc với . Khi chuyển động thì chuyển động trên đường nào ?
Gọi là 2 điểm cố định trên đường tròn tâm , còn điểm chuyển động trên cung lớn của đường tròn. Trên lấy không đổi; Trên lấy không đổi. Chứng minh :
a) luôn bằng chính nó.
b) Đường thẳng song song với vẽ từ điểm đi qua một điểm cố định và đường thẳng tiếp xúc với một đường tròn cố định.
c) Đường cao của đi qua một điểm cố định và trung trực của tiếp xúc với một đường tròn cố định.
Cho hình vuông . Một góc vuông quay cung quanh đỉnh . Đường thẳng cắt đường thẳng theo thứ tự tại ; còn đường thẳng cắt các đường thẳng trên theo thứ tự tại .
Chứng minh là 2 tam giác vuông cân.
Gọi là giao điểm ; còn theo thứ tự là trung điểm của . Tứ giác là hình gì ? Giải thích ?
Chứng minh 4 điểm thẳng hàng. Từ đó có nhận xét gì về đường thẳng khi góc vuông quay quanh ?
Cho đường tròn có là đường kính cố định còn là đường kính thay đổi. Gọi là tiếp tuyến với đường tròn tại . Đường thẳng cắt tại , đường thẳng cắt tại .
Chứng minh tứ giác nội tiếp được một đường tròn.
Chứng minh trung tuyến của vuông góc với .
Tìm tập hợp các tâm của đường tròn ngoại tiếp và tập hợp các trực tâm của .
Cho đường tròn tâm đường kính và điểm di động trên đường tròn . Trên tia lấy điểm sao cho . Dựng hình vuông . Tia cắt đường tròn ở .
Chứng minh là điểm chính giữa cung đồng thời là tâm của đường tròn ngoại tiếp .
Chứng minh tâm đường tròn nội tiếp của và 3 điểm cùng thuộc một đường tròn.
Từ hạ đường cao của . Gọi là bán kính của các đường tròn nội tiếp . Xác định vị trí điểm để tổng đạt giá trị lớn nhất.
Cho đường tròn đường tròn tâm đường kính . Gọi là điểm cố định trên ; là điểm di động trên đường tròn. Qua kẻ đường vuông góc với cắt các tiếp tuyến kẻ từ ở .
Chứng minh vuông.
Chứng minh không đổi.
Chứng minh rằng khi chạy trên đường tròn thì trung điểm của chạy trên một đường thẳng cố định.
Cho cân với nội tiếp đường tròn tâm . là điểm bất kỳ trên đáy . Qua vẽ đường tròn tâm tiếp xúc với tại . Vẽ đường tròn tâm qua tiếp xúc với tại . Gọi là giao điểm thứ hai của 2 đường tròn đó.
Chứng minh rằng thuộc đường tròn tâm .
Chứng minh : luôn đi qua và tích không đổi.
Chứng minh : tổng hai bán kính của 2 đường tròn tâm không đổi.
Tìm tập hợp các trung điểm của .
Chuyên đề 9: BÀI TOÁN HÌNH HỌC TÍNH TOÁN
Cho cân ở và đường tròn tâm có bán kính thay đổi (). Từ kẻ 2 tiếp tuyến với đường tròn. Hai tiếp tuyến này không đối xứng nhau qua trục đối xứng của tam giác và chúng cắt nhau tại .
Chứng minh rằng bốn điểm cùng thuộc một đường tròn. Tìm tập hợp các điểm .
Trên tia đối của tia lấy . Tìm tập hợp điểm .
Chứng minh rằng : .
Cho điểm nằm ngoài đường tròn . Một cát tuyến qua cắt đường tròn tại . Các tiếp tuyến kẻ từ cắt nhau tại . Dựng .
Chứng minh rằng 5 điểm nằm trên đường tròn.
Chứng minh cố định khi cát tuyến quay quanh . Từ đó suy ra tập hợp điểm .
Gọi là trung điểm của và là giao điểm của với . Chứng minh : .
Cho hình thang có đáy lớn .
Phân giác của góc cắt nhau tại , của góc cắt nhau ở . Hỏi có thể là đường trung bình của hình thang được không ? Khi nào ?
Tìm sự liên hệ giữa các cạnh của hình thang khi bốn đường phân giác của các góc đồng quy.
Giả sử đường phân giác của 2 góc cắt nhau tại một điểm thuộc đáy . Tìm hệ thức liên hệ giữa các cạnh của hình thang đã cho.
Cho có 3 góc nhọn nội tiếp trong một đường tròn bán kính .
Chứng minh : .
Chứng minh : .
Cho đoạn thẳng . Gọi là trung điểm của và là đường thẳng trung trực của . Trên lấy một điểm sao cho . Gọi .
Tính theo .
Tiếp tuyến tại của đường tròn có tâm bán kính cắt tại . Tính theo .
Đường tròn tâm bán kính cắt đường tròn ở ; cắt tại . Chứng minh là phân giác của góc và .
Tính theo , theo ? Từ đó suy ra công thức .
Cho nửa đường tròn đường kính , trên đó có một điểm . Trên đường kính có một điểm sao cho . Trên nửa mặt phẳng bờ có chứa điểm ta kẻ các tia vuông góc với . Đường thẳng qua vuông góc với cắt tại . Đường thẳng qua vuông góc với cắt tại . Gọi là giao điểm của và ; là giao điểm của và .
Chứng minh các tứ giác là tứ giác nội tiếp.
Chứng minh .
Chứng minh các điểm thẳng hàng.
Các đường tròn ngoại tiếp và còn có điểm chung nào khác ngoài hay không ?