Đề kiểm tra học kì II môn Toán (Có đáp án) - Năm học 2019-2020 - Trường THCS Nguyễn Bá Ngọc

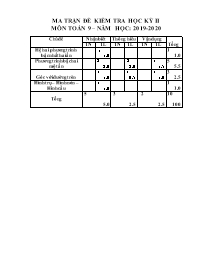
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ II
MÔN TOÁN 9 – NĂM HỌC: 2019-2020
Chủ đề
Nhận biết
Thông hiểu
Vận dụng

Tổng
TN
TL
TN
TL
TN
TL
Hệ hai phương trình bậc nhất hai ẩn

 1 
1.0 




1 
1.0 
Phương trình bậc hai một ẩn

2
2.0 

 2 
2.0

1 
1.5
5
5.5 

Góc với đường tròn

1
1.0

1 
0.5 

1 
1.0
3
2.5
Hình trụ – Hình nón – Hình cầu 

1 
1.0 




1
1.0

Tổng
5
5.0 
 3 
 2.5 
 2 
2.5 
10
10.0

TRƯỜNG THCS NGUYỄN BÁ NGỌC
ĐỀ KIỂM TRA HỌC KỲ II NĂM HỌC 2019 – 2020 
Môn : TOÁN 9
Thời gian làm bài : 90 phút (không kể thời gian phát đề)
ĐỀ CHÍNH THỨC
Bài 1: (2 điểm). Không dùng máy tính, hãy giải phương trình và hệ phương trình sau:
a) ; b) 
Bài 2 : (2điểm). Cho phương trình , trong đó m là tham số.
Với giá trị nào của m thì phương trình trên có nghiệm?
Gọi là hai nghiệm của phương trình trên. Tìm m để 
Bài 3: (2,5điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một tổ công nhân phải làm 144 dụng cụ. Do 3 công nhân chuyển đi làm việc khác nên mỗi người còn lại phải làm thêm 4 dụng cụ. Tính số công nhân lúc đầu của tổ nếu năng suất của mỗi người là như nhau.
Bài 4: (3,5điểm) 
 Cho hình vuông ABCD, lấy một điểm M bất kỳ trên cạnh BC (M khác B và C). 
Qua B kẻ đường thẳng vuông góc với đường thẳng DM tại H, kéo dài BH cắt đường thẳng DC tại K.
Chứng minh tứ giác BHCD nội tiếp đường tròn. Xác định tâm I của đường tròn đó.
Chứng minh .
Chứng minh .
Giả sử hình vuông ABCD có là a. Tính thể tích của hình do nửa hình tròn tâm I quay một vòng quanh đường kính. 
---------------------------------HẾT----------------------------------
DUYỆT CỦA NHÀ TRƯỜNG	 GIÁO VIÊN
 ( Đã ký và đóng dấu)	 ( Đã ký)
 Võ Văn Khương 	 Đỗ Quang Minh
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM MÔN TOÁN 9
HỌC KỲ II – NĂM HỌC 2019 -2020
Bài
Nội dung
Điểm
1a
(1,0đ)
. Ta có 
Vậy PT đã cho có hai nghiệm phân biệt:; 

0,5
0,5
1b
(1,0đ)

Vậy hệ PTđã cho có nghiệm duy nhất 
0,5
0,25
0,25
2a
(1,0đ)
Phương trình có nghiệm 
 (-(2m + 1))2 – 4(m2 + 2) > 0
Vậy với thì PT đã cho có nghiệm
0,25
0,25
0,25
0,25
2b
(1,0đ)
Với , PT đã cho có nghiệm. Theo hệ thức Viét, ta có: 
 và 
Theo đề bài : 
(nhận); (không thỏa điều kiện)
Vậy với thì . 

0,25
0,25
0,25
0,25
3
(2,5đ)

Gọi x (người) là số công nhân của tổ lúc đầu. Điều kiện x nguyên và x
Số dụng cụ mỗi công nhân dự định phải làm là: (dụng cụ)
Số công nhân thực tế khi làm việc là: (người)
Do đó mỗi công nhân thực tế phải làm là: (dụng cụ)
Theo đề bài ta có phương trình: 
Rút gọn, ta có phương trình : 
 (nhận) ; (loại)
Vậy số công nhân lúc đầu của tổ là 12 người.

0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,5
0,25
4a
(1,0đ)

a) Chứng minh tứ giác BHCD nội tiếp
Ta có (vì ABCD là hình vuông)
(vì )
H, C cùng thuộc đường tròn đường kính BD
Vậy tứ giác BHCD nội tiếp được đường tròn 
đường kính BD, có tâm I là trung điểm đoạn BD.

0,25
0,25
0,25
0,25
4b
(0,5đ)
Chứng minh .
Trong có: (đường cao thứ ba)
0,5
4c
(1,0đ)
c) Chứng minh .
 Xét và có: C = H = 900; K là góc chung 
 (g-g)
 (đpcm)

0,25
0,25
0,25
0,25
4d
(1,0đ)
d) Nửa hình tròn tâm I quay một vòng quanh đường kính, ta được một hình cầu có bán kính: .
Trong đó: 
Vậy thể tích của hình cầu là: 
 (đơn vị thể tích). 

0,25
0,25
0,25
0,25

Chú thích: 
Một số bài toán học sinh có thể làm khác nhau nhưng điểm số không được vượt quá thang điểm.
Hình vẽ của bài 4, chỉ phục vụ giải toán, không có điểm số cho hình vẽ.
Điểm bài kiểm tra là tổng điểm của các bài, các phần và được làm tròn đến 0,5đ.
---------------------------------HẾT----------------------------------