Đề kiểm tra học kì II môn Toán Lớp 9 - Đề số 8 (Có đáp án)

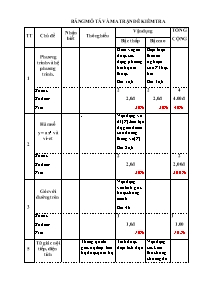
BẢNG MÔ TẢ VÀ MA TRẬN ĐỀ KIỂM TRA
TT
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
TỔNG
CỘNG
Bậc thấp
Bậc cao
1
 Phương trình và hệ phương trình.


Hiểu và giải được các dạng phương trình quen thuộc
Bài 1a,b
Biện luận theo m nghiệm của PT bậc hai
Bài 3 a,b

Số câu:
Số điểm:
Tỉ lệ :


2
2,0đ
20%
2
2,0đ
20%
4
4.00 đ
40%
2
Hàm số 
y = ax2 và vi-et

. 
Vận dụng vẽ đt (P). tìm tọa độ giao điểm của đường thẳng và (P)
Bài 2a,b


Số câu:
Số điểm:
Tỉ lệ :


2
2,0đ
20%

2
2,00đ
20.0%
3
Góc với đường tròn


Vận dụng vào tính góc hoặc chứng minh 
Bài 4 b


Số câu:
Số điểm:
Tỉ lệ :


1
1,0đ
10%

1
1.00
10.%
5
Tứ giác nội tiếp, diện tích

Thông qua tứ giác nội tiếp liên hệ được quan hệ các góc của tứ giác
Chứng minh 2 tích bằng nhau
Bài 4 a
Tính được diện tích dựa vào các điều kiện cơ bản
Bài 4c
Vận dụng các kiến thức trong chương để giải bài toán nâng cao
Bài 4 d

Số câu:
Số điểm:
Tỉ lệ :

1
1.0đ
10%
1
1.0đ
10%
1
1.0đ
10%
03
3.đ
30.0%

TỔNG 
Số câu:
Số điểm:
Tỉ lệ :

0
0,0đ
00%

1
1,0đ
10%

6
6,0đ
40%

3
3,0
30%

10
10,0đ
100%
ĐỀ KIỂM TRA:
Bài 1. ( 2,00 điểm) ( không dùng máy tính cầm tay)
a/ Giải hệ phương trình : 
	b/ Giải phương trình : x4 - x2 – 12 = 0
Bài 2. ( 2,00 điểm)
Trong mặt phẳng Oxy, cho parabol (P) : y = x2 .
	a/ Vẽ đồ thị (P).
	b/ Tìm tọa độ giao điểm của (P) và đường thẳng d: y = -2x +3 bằng phương pháp đại số.
Bài 3. ( 2,00 điểm ) Cho phương trình : x2 – 2(m – 3)x – 4m + 8 = 0 ( m là tham số). 
a/ Chứng minh rằng phương trình luôn có nghiệm .
b/ Gọi x1, x2 là 2 nghiệm phân biệt của phương trình. Tìm giá trị nguyên của m để giá trị biểu thức A = đạt giá trị nguyên.
Bài 4. ( 4,00 điểm)
Cho tam giác ABC nhọn. Hai đường cao BM, CN của ta giác cắt nhau tại H
	a/ Chứng minh : Tứ giác BNMC nội tiếp đường tròn, xác định tâm O của đường tròn đó
	b/ Chứng minh : AB.NM = AM.BC
 c/ Cho biết MC = R, BC = 2R. Tính diện tích hình quạt tròn giới hạn bởi cung nhỏ MC, bán kính OC, bán kính OM của (O) theo R.
d/ Gọi K là giao điểm của AH và BC. I là giao điểm của tia NK và (O). 
 Chứng minh : IM BC
BÀI
ĐÁP ÁN
 ĐIỂM

Bài 1
1a/

Vậy hệ phương trình có một nghiệm duy nhất 
0.25
0.25
0.25
0.25
1b/
x4 - x2 – 12 = 0
Đặt t = x2 , t 0, phương trình trở thành:
t2 - t – 12 = 0
=> phương trình có hai nghiệm phân biệt t = - 3 ( loại) hoặc t = 4 ( nhận)
Với t = 4 x2 = 4 x = -2 hoặc x = 2
Vậy phương trình đã cho có 2 nghiệm 
 x = -2 hoặc x = 2

0.25
0.25
0.25
0.25

Bài 2
2a
Bảng giá trị : 
x
...
-2
-1
0
1
2
...
y= x2
...
4
1
0
1
4
....
 
Đồ thị:
0.25
0.25
0.25
0.25

2b
Phương trình hoành độ giao điểm của d và (P):
x2 = - 2x + 3 x2 +2x - 3 = 0
Pt có dạng a + b + c = 0 nên phương trình có hai nghiệm 
x1 = 1 và x2 = -3. Thay vào phương trình (P) ta được
 y1 = 1, y2 = 9. 
Vậy d cắt (P) tại 2 điểm ( 1;1) hay (-3; 9)
0.25
0.25
0.25
0.25

Bài 3:

 3a

a/ Chứng minh rằng phương trình luôn có nghiệm .
Cho phương trình : 
 x2 – 2(m – 3)x – 4m + 8 = 0 ( m là tham số). 
= (m – 3)2 + 4m – 8 = m2 - 2m +1 
 = (m – 1)2 0 với mọi giá trị của m 
=> Phương trình luôn có nghiệm với mọi giá trị của m

0.50
0.25
0.25
 3b
Pt có hai nghiệm phân biệt > 0 m 1 (*)
Theo định lí vi-et: S = x1+x2 = 2(m-3) 
 P= x1.x2 = – 4m + 8 Do đó: A = =
Với m nguyên, ta có: A nguyên ó nguyên
ó m- 2 Ư(1)={-1, 1}
Do đó : m -2 = -1 ó m = 1 ( loại)
 m -2 = 1 ó m = 3 (nhận) 
Vậy m = 3 thì thỏa mãn yêu cầu bài toán.
0.25
0.25
0.25
0.25

Bài 4:
A
O
C
B
M
N
I
K
H
4a/
Chứng minh : Tứ giác BNMC nội tiếp đường tròn, xác định tâm O của đường tròn đó
=> 
=> Tứ giác BNMC có hai đỉnh liền kề M, N cùng nhìn BC dưới góc 900 nên nội tiếp đường tròn. Tâm O là trung điểm của BC (

0.25
0.25
0.25
0.25
4b/
b/ Chứng minh : AB.NM = AM.BC
 Xét và có :
chung, ( do Tứ giác BNMC nội tiếp đường tròn)
=> đồng dạng ( g.g)
=> 
0.5
0.25
0.25
4c/
c/ Tính diện tích hình quạt tròn giới hạn bởi cung nhỏ MC, bán kính OC, bán kính OM của (O) theo R.
Ta có : OM=OC=MC (=R)=> đều =>
Diện tích của quạt tròn cần tìm: 
( đvdt)
0.25
0.25
0.25
0.25
4d/
Chứng minh : IM BC
Xét tam giác ABC có : BM, CN là hai đường cao cắt nhau tại H => H là trực tâm => AH vuông góc với BC
=> Tứ giác BKHN nội tiếp.
( cùng chắn cung NH)
Lại có : ( cùng chắn cung NB của (O))
=> => AK // IM
 Lại có AK BC 
 => IM BC

0.25
0.25
0.25
 0.25
Thí sinh giải theo cách khác và đúng vẫn cho điểm tối đa.