Đề thi tuyen sinh vào lớp 10 THPT năm học 2011 – 2012
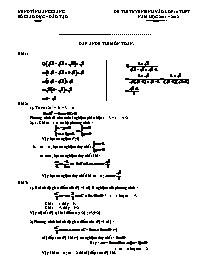
Bài 1:
Bài 2:
1). Ta có : 2x2 – 5x – 3 = 0
Phương trình đã cho có hai nghiệm phân biệt x = 3 v x = -1/2
2). a. Khi m = 1 ta có hệ phương trình :
Vậy hpt có ngiệm (7;4)
b. + m = 0 , hpt có nghiệm duy nhất
+ m 0 , hpt có nghiệm duy nhất khi :
Vậy hpt có ngiệm duy nhất khi m = 0 ;
Bạn đang xem tài liệu "Đề thi tuyen sinh vào lớp 10 THPT năm học 2011 – 2012", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
UBND TÌNH ANG GIANG ĐỀ THI TUYEN SINH VÀO LỚP 10 THPT SỞ GIÁO DỤC – ĐÀO TẠO NĂM HỌC 2011 – 2012 -o0o- -------o0o------- ------------------------------------------------------------------------ ĐÁP ÁN ĐỀ THI MÔN TOÁN. Bài 1: Bài 2: 1). Ta có : 2x2 – 5x – 3 = 0 Phương trình đã cho có hai nghiệm phân biệt x = 3 v x = -1/2 2). a. Khi m = 1 ta có hệ phương trình : Vậy hpt có ngiệm (7;4) b. + m = 0 , hpt có nghiệm duy nhất + m 0 , hpt có nghiệm duy nhất khi : Vậy hpt có ngiệm duy nhất khi m = 0 ; Bài 3: 1). Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình : ó x = 1 hoặc x = -3 + Khi x = 1 thì y = ½ + Khi x = -3 thì y = 9/2 Vậy (d) cắt (P) tại hai điểm (1;1/2) ; (-3;9/2) 2) Phương trình hoành độ giao điểm cùa (P) và (d/) : (*) (d/) tiếp xúc (P) khi (*) có nghiệm duy nhất : Hay : ó m = 0 hoặc m = 2 Vậy khi m = 0 ; m = 2 thì (d/) tiếp xúc (P) khi. Bài 4. 1). Xét tứ giác ODNM, ta có : = ½ sđ ( gt) Do đó : Hay tứ giác ODNM nội tiếp 2). Xét và , ta có : sđ () Do đó : Hay : AN.MB = AC.MN 3). Vì OD = ON = DN = r nên Hay : Suy ra : ( chắn cung AND bằng 1500 ) Suy ra : Áp dụng hệ thức lượng giác trong tam giác vuông AOE, ta có : tg150 = => OE = 0,27r Do đó : ED = OD – OE = r – 0,27r = 0,73r EC = OC + OE = r + 0,27r = 1,27r. --- HẾT ---
Tài liệu đính kèm:
 DAP AN DE THI TUYEN SINH LOP 10 1112 TINH AG.doc
DAP AN DE THI TUYEN SINH LOP 10 1112 TINH AG.doc





