Kiểm tra 45 phút học kì II năm học: 2009 - 2010 môn Hình học lớp 9

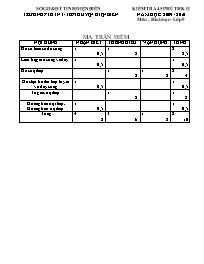
MA TRẬN ĐIỂM
NỘI DUNG
NHẬN BIẾT
THÔNG HIỂU
VẬN DỤNG
TỔNG
Góc ở tâm số đo cung
1
0,5
1
2
2
2,5
Liên hệ giữa cung và dây
1
0,5
1
0,5
Góc nội tiếp
1
2
1
2
2
4
Góc tạo bởi tia tiếp tuyến và dây cung
1
0,5
1
0,5
Tứ giác nội tiếp
1
2
1
2
Đường tròn nội tiếp. Đường tròn nội tiếp
1
0,5
1
0,5
Tổng
4
2
3
6
1
2
8
10
ĐỀ SỐ 1:
Họ và tên :..
 Lớp :..
Điểm
Lời phê của giáo viên
Đề bài:
Câu 1: Điền vào ô trống chữ Đ nếu cho là đúng, chữ S nếu cho là sai:
a) Trong một đường tròn các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn các góc nội tiếp bằng nhau thì cùng chắn một cung.
c) Trong một đường tròn các góc nội tiếp bằng nhau thì chắn các cung bằng nhau.
d) Góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
Câu 2: Góc ở tâm là gì ? Phát biểu định lí về góc tạo bởi tiếp tuyến và dây cung.
Câu 3: Cho tam giác ABC vuông ở A, trên AC lấy điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S 
(S nằm giữa A và D) CMR:
ABCD là một tứ giác nội tiếp.
Góc ABD = góc ACD.
CA là phân giác của góc SCB.
BÀI LÀM
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................
..........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................
 ĐÁP ÁN VÀ BIỂU ĐIỂM (ĐỀ 1)
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1
a) Đ
b) Đ
c) S
d) Đ
2đ
Câu 2
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
1đ
1đ
Câu 3
Gt
∆ABC vuông tại A, Vẽ (O,), BM(O)=D DA (O) = S(S nằm giữa A và D) 
Kl
ABCD là một tứ giác nội tiếp.
b)Góc ABD = góc ACD.
c)CA là phân giác của SCB
 C
D
B
A
S
M
O
a) Có góc MDC = 900 (góc nội tiếp chắn nửa đường tròn)
Có góc BAC = 900 (giả thiết )	
Điểm A và D đều nhìn đoạn thẳng BC cố định dưới góc 900 
Vậy Avà D cùng nằm trên đường tròn đường kính BC hay tứ giác ABCD nội tiếp đường tròn đường kính BC	
b) Trong đường tròn đường kính BC có góc ABD = góc ACD ( vì cùng chắn cung AD) 	
c) Góc SDM = góc MCS (1) ( cùng chắn cung MS của đường tròn tâm (o)
Lại có góc ADB = góc ACB (2) cùng chắn cung AB của đường tròn đường kính BC)	
Từ (1) và (2) => góc SCM = góc ACB hay góc SCA = góc ACB =>CA là tia phân giác của góc SCB	
1đ
0,5đ
0,5đ
1đ
1đ
0,5đ
0,5đ
1đ
ĐỀ SỐ 2:
Họ và tên :..
 Lớp :..
Điểm
Lời phê của giáo viên
Đề bài:
Câu 1: Điền vào ô trống chữ Đ nếu cho là đúng, chữ S nếu cho là sai:
 Tứ giác ABCD nội tiếp được trong một đường tròn nếu có một trong các điều kiện sau:
a) góc DAB = góc DCB = 900
b) góc ABC = góc CDA = 1800
c) góc DAC = gócDBC = 600
d) góc DAB = gócDCB = 600
Câu 2: Góc tạo bởi tia tiếp tuyến và dây cung là gì ? Phát biểu định lí về đường tròn ngoại tiếp và đường tròn nội tiếp của đa giác đều.
Câu 3: Cho hình vuông ABCD, điểm E BC. Qua B kẻ đường thẳng vuông góc với DE, đường vuông góc đó cắt DE ở H và cắt DC ở K.
CMR: Tứ giác BHCD nội tiếp.
Tính số đo của góc CHK.
CMR: KC.KD = KH.KB.
BÀI LÀM
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................
......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................... ĐÁP ÁN VÀ BIỂU ĐIỂM (ĐỀ 2)
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1
a) Đ
b) Đ
c) Đ
d) S
2đ
Câu 2
Góc tạo bởi tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tiếp tuyến và cạnh kia chứa dây cung
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
1đ
1đ
Câu 3
Gt
Hình vuông ABCD; E BC; DE BH = H
BH CD = {K}
Kl
a)Tứ giác BHCD nội tiếp 
b) Tính góc CHK
c) CMR: KC. KD = KH . KB
Giải:
a) Ta có góc BCD = 900 (ABCD là hình vuông) 
C đường tròn đường kính BD 
Góc BHD = 900 (DE BH = H) 
H đường tròn đường kính BD 
 C, H, B, D cùng thuộc một đường tròn
 Tứ giác BHCD nội tiếp
b) Góc DBC = 450 (tính chất hình vuông) (1 ) 
Góc DBC = góc DHC (cùng chắn một cung DC) (2) 
Từ (1) và (2) góc DHC = 450 (*) 
Mặt khác góc DHC + góc CHK = 900 (**) 
Từ (*) và (**) góc CHK = 450 
c) Xét KCH và KDB
Có chung
CHK = BKD = 450
 KCH KDB ( G - G) 
KC . KD = KB . KH (ĐPCM) 
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
ĐỀ SỐ 3:
Họ và tên :..
 Lớp :..
Điểm
Lời phê của giáo viên
Đề bài:
Câu 1: Điền dấu “X” thích hợp vào ô trống.
Câu
Nội dung
Đúng 
Sai
a
Hình vuông nội tiếp được một đường tròn.
b
Tổng số đo của 2 góc đối diện trong một tứ giác nội tiếp bắng .
c
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
d
Trong một đường tròn góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 2: Góc nội tiếp là gì ? Phát biểu định nghĩa tứ giác nội tiếp đường tròn. 
Câu 3: Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (0). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB tại D và E.
CMR: BD2 = AD . CD.
Tứ giác BCDE là tứ giác nội tiếp.
BC // DE.
BÀI LÀM
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................
................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................ ... .......................................................................................................................................................................................................................
.........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................ĐÁP ÁN VÀ BIỂU ĐIỂM (ĐỀ 4)
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1
a) Đ
b) Đ
c) S
d) Đ
2đ
Câu 2
Góc tạo bởi tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tiếp tuyến và cạnh kia chứa dây cung
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
1đ
1đ
Câu 3
Gt
∆ABC: AB=AC > BC, nội tiếp (0). Tiếp tuyến tại B và C của (0) lần lượt cắt tia AC và tia AB tại D và E.
Kl
a)CMR: BD2 = AD . CD.
b)Tứ giác BCDE là tứ giác nội tiếp.
c) BC // DE.
a) ADB ~ BDC (gg) 	
=> 	
=> BD2 = AD . CD	
b) Theo định lí góc có đỉnh ở bên ngoài đường (0) ta CM được 
E1 = D1 	
=> BCDF nội tiếp	
c) CM ABC = BED (cùng bù với góc BCD)=> BC // ED
0,5đ
0,5đ
0,5đ
0,5đ
2đ
1đ
1đ
ĐỀ SỐ 5:
Họ và tên :..
 Lớp :..
Điểm
Lời phê của giáo viên
Đề bài:
Câu 1: Điền vào ô trống chữ Đ nếu cho là đúng, chữ S nếu cho là sai:
 Tứ giác ABCD nội tiếp được trong một đường tròn nếu có một trong các điều kiện sau:
a) góc DAB = góc DCB = 900
b) góc ABC = góc CDA = 1800
c) góc DAC = gócDBC = 600
d) góc DAB = gócDCB = 600
Câu 2: Góc nội tiếp là gì ? Phát biểu định nghĩa tứ giác nội tiếp đường tròn. 
Câu 3: Cho tam giác ABC vuông ở A, trên AC lấy điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S (S nằm giữa A và D) CMR:
ABCD là một tứ giác nội tiếp.
b) Góc ABD = góc ACD.
c) CA là phân giác của góc SCB.
BÀI LÀM
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................... ĐÁP ÁN VÀ BIỂU ĐIỂM (ĐỀ 5)
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1
a) Đ
b) Đ
c) Đ
d) S
2đ
Câu 2
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa 2 dây cung của đường tròn đó
Một tứ giác có 4 đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn
1đ
1đ
Câu 3
Gt
∆ABC vuông tại A, Vẽ (O,), BM(O)=D DA (O) = S(S nằm giữa A và D) 
Kl
ABCD là một tứ giác nội tiếp.
b)Góc ABD = góc ACD.
c)CA là phân giác của SCB
 C
D
B
A
S
M
O
a) Có góc MDC = 900 (góc nội tiếp chắn nửa đường tròn)
Có góc BAC = 900 (giả thiết )	
Điểm A và D đều nhìn đoạn thẳng BC cố định dưới góc 900 
Vậy Avà D cùng nằm trên đường tròn đường kính BC hay tứ giác ABCD nội tiếp đường tròn đường kính BC	
b) Trong đường tròn đường kính BC có góc ABD = góc ACD ( vì cùng chắn cung AD) 	
c) Góc SDM = góc MCS (1) ( cùng chắn cung MS của đường tròn tâm (o)
Lại có góc ADB = góc ACB (2) cùng chắn cung AB của đường tròn đường kính BC)	
Từ (1) và (2) => góc SCM = góc ACB hay góc SCA = góc ACB =>CA là tia phân giác của góc SCB	
1đ
0,5đ
0,5đ
1đ
1đ
0,5đ
0,5đ
1đ
ĐỀ SỐ 6:
Họ và tên :..
 Lớp :..
Điểm
Lời phê của giáo viên
Đề bài:
Câu 1: Điền dấu “X” thích hợp vào ô trống.
Câu
Nội dung
Đúng 
Sai
a
Hình vuông nội tiếp được một đường tròn.
b
Tổng số đo của 2 góc đối diện trong một tứ giác nội tiếp bắng .
c
Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
d
Trong một đường tròn góc nội tiếp chắn nửa đường tròn là góc vuông.
Câu 2: Góc ở tâm là gì ? Phát biểu định lí về góc tạo bởi tiếp tuyến và dây cung.
Câu 3: Cho hình vuông ABCD, điểm E BC. Qua B kẻ đường thẳng vuông góc với DE, đường vuông góc đó cắt DE ở H và cắt DC ở K.
CMR: Tứ giác BHCD nội tiếp.
Tính số đo của góc CHK.
CMR: KC.KD = KH.KB.
BÀI LÀM
.....................................................................................................................................................................................................................................................................................................................................................................................................................................................
.......................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................ĐÁP ÁN VÀ BIỂU ĐIỂM (ĐỀ 6)
CÂU
ĐÁP ÁN
BIỂU ĐIỂM
Câu 1
a) Đ
b) Đ
c) S
d) Đ
2đ
Câu 2
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
1đ
1đ
Câu 3
Gt
Hình vuông ABCD; E BC; DE BH = H
BH CD = {K}
Kl
a)Tứ giác BHCD nội tiếp 
b) Tính góc CHK
c) CMR: KC. KD = KH . KB
Giải:
a) Ta có góc BCD = 900 (ABCD là hình vuông) 
C đường tròn đường kính BD 
Góc BHD = 900 (DE BH = H) 
H đường tròn đường kính BD 
 C, H, B, D cùng thuộc một đường tròn
 Tứ giác BHCD nội tiếp
b) Góc DBC = 450 (tính chất hình vuông) (1 ) 
Góc DBC = góc DHC (cùng chắn một cung DC) (2) 
Từ (1) và (2) góc DHC = 450 (*) 
Mặt khác góc DHC + góc CHK = 900 (**) 
Từ (*) và (**) góc CHK = 450 
c) Xét KCH và KDB
Có chung
CHK = BKD = 450
 KCH KDB ( G - G) 
KC . KD = KB . KH (ĐPCM) 
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ