Một số kiến thức cần nhớ và kiến thức bổ xung môn Toán
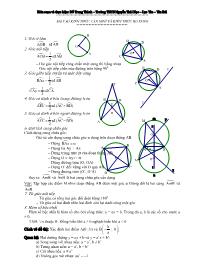
1. Góc ở tâm
A·OB = sđ A»B
2. Góc nội tiếp
A·CB 1
2
= sđ A»B
– Hai góc nội tiếp cùng chắn một cung thì bằng nhau
– Góc nội tiếp chắn nửa đường tròn bằng 900
3. Góc giữa tiếp tuyến và một dây cung
· 1
BAx
2
= sđ A»B
· 1
CAy
2
= sđ C»A
4. Góc có đỉnh ở bên trong đường tròn
· 1
AEC
2
= sđ (A»C + B»D)
Bạn đang xem tài liệu "Một số kiến thức cần nhớ và kiến thức bổ xung môn Toán", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Biên soạn và thực hiện: Đỗ Trung Thành – Trường THCS Nguyễn Thái Học – Lục Yên – Yên Bái ********************************************************************* E D B C F A MỘT SỐ KIẾN THỨC CẦN NHỚ VÀ KIẾN THỨC BỔ XUNG ********************************** 1. Góc ở tâm · AOB = sđ » AB 2. Góc nội tiếp · 1 ACB 2 = sđ » AB – Hai góc nội tiếp cùng chắn một cung thì bằng nhau – Góc nội tiếp chắn nửa đường tròn bằng 90 0 3. Góc giữa tiếp tuyến và một dây cung · 1 BAx 2 = sđ » AB · 1 CAy 2 = sđ » CA 4. Góc có đỉnh ở bên trong đường tròn · 1 AEC 2 = sđ » » (AC BD) + 5. Góc có đỉnh ở bên ngoài đường tròn · 1 AFC 2 = sđ » » (AC BD) - 6. Quĩ tích cung chứa góc Cách dựng cung chứa góc: Giả sử cần dựng cung chứa góc α dựng trên đoạn thẳng AB – Dựng · BAx = a – Dựng tia Ay ^ Ax – Dựng trung trực zt của đoạn thẳng AB – Dựng O ≡ Ay Ç zt – Dựng đường tròn (O, OA) – Dựng O’ đối xứng với O qua AB – Dựng đường tròn (O’, O’A) Suy ra: ¼ AmB và ¼ AnB là hai cung chứa góc cần dựng Vậy: Tập hợp các điểm M nhìn đoạn thẳng AB dưới một góc α không đổi là hai cung ¼ AmB và ¼ AnB 7. Tứ giác nội tiếp – Tứ giác có tổng hai góc đối diện bằng 180 0 – Tứ giác có hai đỉnh nhìn hai đỉnh còn lại dưới cùng một góc 8. Hàm số bậc nhất Hàm số bậc nhất là hàm số cho bởi công thức: y = ax + b. Trong đó a, b là các số cho trước a ≠ 0. TXĐ: "x thuộc R. Đồng biến khi a ≥ 0 nghịch biến khi a < 0 Cách vẽ đồ thị: Xác định hai điểm A(0 ; b) và b B ; 0 a æ ö - ç ÷ è ø Quan hệ: Hai đường thẳng y = ax + b và y = a’x + b’: a) Song song với nhau nếu: a = a’, b ≠ b’ b) Trùng nhau nếu: a = a’, b = b’ c) Cắt nhau nếu: a ≠ a’ d) Vuông góc với nhau: aa’ = –1 O A B O A B D C y x O A B D C a t z y x n m O' O A B M M A B C D Biên soạn và thực hiện: Đỗ Trung Thành – Trường THCS Nguyễn Thái Học – Lục Yên – Yên Bái ********************************************************************* 5) Hệ số góc: a là hệ số góc của đường thẳng y = ax + b Trong đó: a = tgα (α là góc tạo bởi góc giữa đường thẳng y = ax + b và trục hoành Ox) 6) Tọa độ trung điểm M(xM ; yM) của đoạn thẳng AB với A(xA ; yA) và B(xB ; yB) A B A B M M x x y y x ; y 2 2 + + = = 7) Độ dài đoạn thẳng AB: 2 2 A B A B AB (x x ) (y y ) = - + - 9. Hàm số y = ax 2 a) Cách vẽ đồ thị: Đồ thị của hàm số luôn đi qua gốc tọa độ, nằm bên trên trục hoành khi a > 0 và nằm bên dưới trục hoành nếu a < 0. Chú ý: đồ thị hàm số luôn đối xứng với nhau qua trục tung Oy b) Tính chất biến thiên: TXĐ: "x thuộc R – Nếu a > 0: Nghịch biến khi x 0 – Nếu a 0 10. Phương trình bậc hai ax 2 + bx + c = 0 (a ≠ 0) a) Công thức nghiệm Xây dựng công thức nghiệm của phương trình bậc hai ax 2 + bx + c = 0 (1) (a ≠ 0) (1) Û 2 b c x x 0 a a + + = Û 2 2 2 2 2 b b b c x 2. .x 0 2a 4a 4a a + + - + = Û 2 2 2 b b 4ac x 0 2a 4a - æ ö + - = ç ÷ è ø Đặt Δ = b 2 – 4ac: phương trình trở thành: 2 2 b x 0 2a 4a D æ ö + - = ç ÷ è ø – Nếu Δ < 0: phương trình vô nghiệm – Nếu Δ = 0: (1) Û 2 b x 0 2a æ ö + = ç ÷ è ø phương trình có nghiệm kép: 1 2 b x x 2a = = - – Nếu Δ > 0: (1) Û b b x x 0 2a 2a æ öæ ö - D + D + + = ç ÷ç ÷ ç ÷ç ÷ è øè ø Phương trình có hai nghiệm phân biệt: 1 b x 2a - + D = 2 b x 2a - - D = Đặt Δ = b 2 – 4ac – Nếu Δ < 0: phương trình vô nghiệm – Nếu Δ = 0: phương trình có nghiệm kép 1 2 b x x 2a = = - – Nếu Δ > 0: phương trình có hai nghiệm phân biệt 1 2 b b x ; x 2a 2a - + D - - D = = Ví dụ: Giải phương trình 3x 2 – 5x – 6 = 0 Δ = 5 2 + 4.3.6 = 25 + 72 = 97 Phương trình có hai nghiệm phân biệt: Biên soạn và thực hiện: Đỗ Trung Thành – Trường THCS Nguyễn Thái Học – Lục Yên – Yên Bái ********************************************************************* 1 2 5 97 5 97 x ; x 6 6 + - = = Nhận xét: Nếu ac < 0 thì phương trình bậc hai luôn có hai nghiệm phân biệt b) Định lí Viet & Ứng dụng của định lí Viet Định lí: Nếu phương trình ax 2 + bx + c = 0 có hai nghiệm x1, x2 thì: 1 2 2 2 b x x a c x x a ì + = - ï ï í ï = ï î Định lí đảo: Nếu hai số a, b thỏa mãn điều kiện a b S ab P + = ì í = î thì a, b là nghiệm của phương trình x 2 – Sx + P = 0 Ứng dụng: Nhẩm nghiệm của phương trình bậc hai – Nếu phương trình có a + b + c = 0 thì x1 = 1 và 2 c x a = – Nếu phương trình có a – b + c = 0 thì x1 = –1 và 2 c x a = - – Ngoài ra có thể đoán nhận nghiệm của phương trình bậc hai thông qua tìm tổng và tích hai nghiệm 12. Một số bài tập áp dụng: 1. Vẽ các Parabol y = x 2 , y = –x 2 , y = 2x 2 , y = –2x 2 trên cùng một hệ trục tọa độ Giải: Hàm số y = x 2 . lập bảng biến thiên: x –3 –2 –1 0 1 2 3 y = x 2 9 4 1 0 1 4 9 Hàm số y = –x 2 . lập bảng biến thiên x –3 –2 –1 0 1 2 3 y = x 2 –9 –4 –1 0 –1 –4 –9 Hàm số y = 2x 2 . lập bảng biến thiên: x –3 –2 –1 0 1 2 3 y = 2x 2 18 8 2 0 2 8 18 Hàm số y = –2x 2 . lập bảng biến thiên: x –3 –2 –1 0 1 2 3 y = 2x 2 –18 –8 –2 0 –2 –8 –18 2. Trong mặt phẳng tọa độ Oxy cho các đường thẳng: (d1): y = 2x + 3 (d2): y = –x + 2 (d3): y = 0,5x – 2 a) Vẽ ba đường thẳng trên hệ trục tọa độ Oxy b) Gọi A ≡ (d1) Ç (d2), B ≡ (d1) Ç (d3), C ≡ (d2) Ç (d3). Xác định tọa độ của A, B, C c) Gọi M, N, P là trung điểm của BC, AC và AB. Xác định tọa độ của M, N, P Biên soạn và thực hiện: Đỗ Trung Thành – Trường THCS Nguyễn Thái Học – Lục Yên – Yên Bái ********************************************************************* d) Gọi AD, AH lần lượt là đường phân giác, đường cao của tam giác ABC. Lập phương trình các đường thẳng AD, AH và trung tuyến AM của tam giác ABC 3. Dùng công thức nghiệm để giải các phương trình sau: a) 2 x 5x 7 0 + + = b) 4x 2 + 12x + 9 = 0 c) 3x 2 – 4x – 5 = 0 d) 2 2x ( 2 2)x 2 0 - - - = 4. Tìm hai số u, v trong mỗi trường hợp sau: a) u + v = 30 và uv = 125 b) u – v = 5 và uv = 24 c) u 2 + v 2 = 25 và u + v = 7 d) u 3 + v 3 = 152 và uv = 15 5. Biết rằng phương trình 2 x 3x 5 0 - - = có hai nghiệm phân biệt x1, x2. Không giải phương trình hãy tính: a) 2 2 1 2 x x + b) 1 2 1 1 x x + c) 3 3 1 2 x x + d) 2 2 1 2 1 x x +
Tài liệu đính kèm:
 Mot so kien thuc ghi nho doi voi HS Lop 9.pdf
Mot so kien thuc ghi nho doi voi HS Lop 9.pdf





