Đề kiểm tra học kì II môn Toán (Có đáp án) - Trường THCS Huỳnh Thúc Kháng

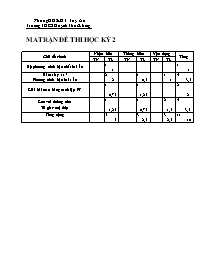
 Phòng GD&ĐT Tuy An
Trường THCS Huỳnh Thúc Kháng
MA TRẬN ĐỀ THI HỌC KỲ 2
Chủ đề chính
Nhận biết
Thông hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
Hệ phương trình bậc nhất hai ẩn


1
 1




1
 1
Hàm số y=ax2
Phương trình bậc hai 1 ẩn

2
 2

1
 0,5

1
 1
4
 3,5
Giải bài toán bằng cách lập PT

1
 0,75

1
 1,25


2
 2
Góc với đường tròn
Töù giaùc noäi tieáp

1
 1,25

1
 0,75

2
 1,5
4
 3,5
Tổng cộng


5 
 5

3 
 2,5

3
 2,5
11
 10
 
 Phòng GD&ĐT Tuy An
Trường THCS Huỳnh Thúc Kháng
ĐỀ KIỂM TRA HỌC KỲ 2
MÔN TOÁN: 9
Thời gian : 90 phút
------------------------------------------------------------------------------------------------------------------
Bài 1:
Không sử dụng máy tính cầm tay, hãy giải phương trình và hệ phương trình sau:
a)
b)
Bài 2:
Một người dự định đi xe máy từ A đến B cách nhau 90km. Vì có việc gấp phải đến B trước dự định 45 phút nên người ấy tăng vận tốc lên mỗi giờ 10km. Hãy tính vận tốc mà người ấy dự định đi.
Bài 3:
a)Vẽ đồ thị hàm số : và y = x lên cùng một hệ trục tọa độ. Hãy tìm tọa độ giao điểm của chúng bằng phép tính.
b)Cho phương trình: x2 - 2(m+1)x + 2m = 0, x1; x2 là hai nghiệm của phương trình, Hãy tìm giá trị của m để biểu thức đạt giá trị nhỏ nhất.
Bài 4:
Cho đường tròn (O;R) có đường kính BC. Gọi A là điểm nằm trên đường tròn sao cho AB > AC. Trên tia đối AC lấy điểm P sao cho AP = AB. Đường thẳng vuông góc hạ từ P xuống BC cắt BA ở D và cắt BC tại H.
Chứng minh: tứ giác ACHD nội tiếp
Chứng minh: PC . PA = PH . PD
PB cắt (O) tại I. Chứng minh các điểm I; C; D thẳng hàng.
Cho góc . Hãy tính theo R diện tích của hình tròn ngoại tiếp tứ giác ACHD
 Phòng GD&ĐT Tuy An
Trường THCS Huỳnh Thúc Kháng
ĐÁP ÁN 
MÔN TOÁN: 9
Thời gian : 90 phút
------------------------------------------------------------------------------------------------------------------
Bài 1:
Không sử dụng máy tính cầm tay, hãy giải phương trình và hệ phương trình sau:
a)
 	(0,5đ)
Vậy phương trình có hai nghiệm phân biệt:
 ; 	(0,5đ)
b)	(0,5đ)
Vậy hệ phương trình có nghiệm (x;y) = (2; -3) 	(0,5đ)
Bài 2:
Gọi vận tốc dự định của người đi xe máy từ A đến B là: x (km/h) ; x > 0
 Vận tốc thực tế đi từ A đến B của người ấy là: x + 10 (km/h) 	(0,25đ) 
 Thời gian dự định đi từ A đến B của người ấy là: (giờ)
 Thời gian thực tế đi từ A đến B của người ấy là: (giờ)	(0,25đ)
 Vì đến trước dự định 45 phút nên ta có phương trình :
	(0,5đ)
 Qui đồng khử mẫu ta được phương trình bậc hai :
	 x2 +10x – 1200 = 0	(0,5đ)
Giải phương trình ta được: (Loại)
 Vậy vận tốc dự định của người đi xe máy từ A đến B là: 30km/h	(0,5đ)
Bài 3:
a)Vẽ đồ thị hàm số : (P) và y = x (d)	
Vẽ đúng mỗi đồ thị hàm số được (0,5đ)
Tìm tọa độ giao điểm của chúng bằng phép tính.
Hoành độ giao điểm của (P) và (d) là : 	(0,25đ)
	Þx1 = 0 ; y1=0
	 x2 = 2 ; y2 =2
Vậy tọa độ giao điểm của chúng là : (0;0) ; (2;2)	(0,25đ)
b)Cho phương trình: x2 - 2(m+1)x + 2m = 0, x1; x2 là hai nghiệm của phương trình, Hãy tìm giá trị của m để biểu thức đạt giá trị nhỏ nhất.
	(0,25đ)
Do đó phương trình đã cho luôn có 2 nghiệm phân biệt.
	(0,5đ)
Vậy: m = thì biểu thức đạt giá trị nhỏ nhất.	(0,25đ)
Bài 4:
Hình vẽ, gt, kl : 0,5đ
a)Chứng minh: tứ giác ACHD nội tiếp
Xét tứ giác ACHD có : 	(0,25đ)
(góc nội tiếp chắn nửa đường tròn)	(0,25đ)
Do đó : 
Vậy tứ giác ACHD nội tiếp	(0,25đ)
b)Chứng minh: PC . PA = PH . PD
DADP và DHCP có : 
	Góc P : chung	(0,25đ)
Nên DADP DHCP do đó 	(0,5đ)
c)PB cắt (O) tại I. Chứng minh các điểm I; C; D thẳng hàng.
(góc nội tiếp chắn nửa đường tròn) hay CI ^ BP (1)	(0,25đ)
Xét tam giác BCP có đường cao BA, PH cắt nhau tại D 
Do đó : CD ^ BP (Đường cao thứ 3) (2)	(0,25đ)
Từ (1) và (2) suy ra C ; D; I thẳng hàng 	(0,25đ)
d)Cho góc . Hãy tính theo R diện tích của hình tròn ngoại tiếp tứ giác ACHD
	Tam giác ABP vuông cân tại A nên 
	Tam giác vuông ICP có nên DICP vuông cân tại I do đó 
(0,25đ)
	Tam giác vuông ACD có nên DACD vuông cân tại A suy ra: AC=AD
	Mà nên AC = AD =R suy ra CD=	(0,25đ)
Vậy diện tích hình tròn ngoại tiếp tứ giác ACHD là : 
(đvdt)	(0,25đ)