Ôn tập Hình học năm 200 9 - 2010
A.LÝ THUYẾT
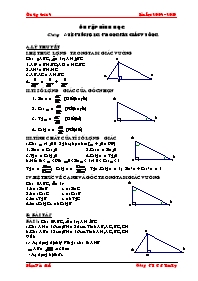
I.HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Cho ABC, = 1v; AHBC
1.AB2 = BH.BC; AC2 = HC.BC
2.AH2 = BH.HC
3.AB.AC = AH.BC
4. = +
II.TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN
1.
Sin = (Đối/huyền)
2. Cos = (Kề/huyền)
3. Tg = (Đối/kề)
4.
Cotg = (Kề/đối)
III.TÍNH CHẤT CỦA TỈ SỐ LƯỢNG GIÁC
a.Cho và là 2 góc phụ nhau ( + = 900)
1. Sin = Cos 2.Cos = Sin
3.Tg = Cotg 4.Cotg = Tg
b.Nếu 00<>< 900=""><>< 1="" và=""><><>
Tg = ; Cotg = ; Tg.Cotg = 1; Sin2 + Cos2 = 1
Bạn đang xem 20 trang mẫu của tài liệu "Ôn tập Hình học năm 200 9 - 2010", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ôn tập hình học Chương I: Hệ thức lượng trong tam giác vuông a.Lý thuyết I.Hệ thức lượng trong tam giác vuông Cho ABC, = 1v; AHBC 1.AB2 = BH.BC; AC2 = HC.BC 2.AH2 = BH.HC 3.AB.AC = AH.BC 4. = + II.Tỉ số lượng giác của góc nhọn Sin = (Đối/huyền) Cos = (Kề/huyền) Tg = (Đối/kề) Cotg = (Kề/đối) III.Tính chất của tỉ số lượng giác a.Cho và là 2 góc phụ nhau ( + = 900) 1. Sin = Cos 2.Cos = Sin 3.Tg = Cotg 4.Cotg = Tg b.Nếu 00< < 900 0< Sin< 1 và 0< Cos<1 Tg = ; Cotg = ; Tg.Cotg = 1; Sin2 + Cos2 = 1 IV.Hệ thức về cạnh và góc trong tam giác vuông: Cho ABC, = 1v 1.b = aSinB c = aSinC 2.b = aCosC c = aCosB 3.b= cTgB c = bTgC 4.b= cCotgC c = bCotgB B: Bài tập Bài 1: Cho ABC, = 1v; AHBC a.Cho AH = 16cm; BH = 25cm. Tính AB, AC, BC, CH b.Cho AB = 12cm; BH = 16cm. Tính AH, AC, BC, CH Giải: a.- áp dụng định lý Pitago cho vAHB AB = 30cm - áp dụng hệ thức AH2 = HB.HC HC = = = BC = CH + HB = - áp dụng hệ thức AC2 = CH.BC AC = 19cm b.Tính tương tự Bài 2: Cho ABC vuông tại A, AB = 30cm, đường cao AH = 24cm. a.Tính độ dài BH. b.Tính độ dài BC. c.Qua B kẻ đường thẳng song song với AC cắt đường thẳng AH tại D. Tính độ dài BD. Giải a.- áp dục định lý Pitago cho vABH BH = 18cm. áp dụng hệ thức AB2 = BH.BC BC = = = 50cm Cách 1: Chứng minh BAD vuông tại B có BH AD - áp dụng hệ thức: BH2 = AH.HD HD = = = AD = AH + HD = - áp dụng hệ thức BD2 = HD.AD BD = 22,5cm Cách 2: Chứng minh HBDHAB BD = 22,5cm Bài 3: Cho Cho ABC, = 1v; AB = 6dm, AC = 8dm, các đường phân giác góc trong và góc ngoài của cắt AC ở M và N. Tính AM và AN. Giải: - áp dụng định lý Pitago chovABC BC = 10cm. áp dụng tính chất đường phân giác trong tam giác ta có : = = = = AM = AM = 3cm - áp dụng hệ thức cho vMBN ta có: AB2 = AM.AN AN = = = = 12 (cm) Bài 4: Cho ABC các góc đều nhọn. Trên đường cao AD lấy điểm P sao cho = 900. Trên đường cao BE lấy điểm Q sao cho = 900. Chứng minh rằng: a.CA.CE = CD.CB b.CP = CQ Giải: a.Chứng minh CDACEB = CE.CA = CD.CB b.áp dụng hệ thức vBPC PC2 = CD.CB áp dụng hệ thức vAQC CQ2 = CE.CA Mà CD.CB = CE.CA (CMT) CP2 = CQ2 CP = CQ Bài 5.Cho ABC có AB = 21cm, AC = 28cm, BC = 35cm. a.Chứng minh ABC vuông. Tính SABC b.Tính SinB, SinC c.Đường phân giác của cắt BC tại D. Tính DB, DC Giải: a.áp dụng định lý đảo Pitago BC2 = AB2 + AC2 ABC vuông tại A. SABC = AB.AC = .21.28 = 294cm2 b.SinB = = = Sin C = = = c.áp dụng tính chất đường phân giác: = = = DB = 15 DC = 20 Bài 6: Cho ABC vuông ở A, có AB = 6cm, AC = 8cm. a.Tính BC, góc B, góc C. b.Đường phân giác của cắt BC tại D. Tính DB, DC. c.Từ D kẻ DEAB, DFAC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF. Giải: (Tương tự như bài 5) Bài 7: Cho hình thang ABCD có cạnh bên là AD và BC bằng nhau, đường chéo AC vuông góc với cạnh bên BC. Biết AD = 5 và AC = 12 a.Tính b.Tính chiều cao của hình thang ABCD Giải: a.áp dụng định lý Pitago cho vACB AB2 = AC2 + BC2 = 25 + 144 = 169 AB = 13 SinB = = ; CosB = = Vậy = = = b.áp dụng hệ thức lượng cho vACB AC.CB = CH.AB CH = = = Bài 8: Cho hình thang ABCD, đáy AB = 2, đáy CD = 4. Cạnh bên AD = 2, góc = 900 a.Chứng minh TgC = 1 b.Tính tỉ số diện tích DBC và diện tích hình thang ABCD c.Tính tỉ số diện tích ABC và diện tích DBC Giải: a.Kẻ BHDC (HDC) Tứ giác ABHD là hình vuông. BH = DH = 2 HC = DC – DH = 4 – 2 = 2 Xét vAHC TgC = = = 1 b.Ta có SDBC = BH.DC = .2.4 = 4 SABCD = (AB + DC).BH = (2 + 4).2 = 6 = = Bài 9: Cho ABC vuông ở A, = 300, BC = 10cm a.Tính AB, AC. b.Từ A kẻ AM và AN vuông góc với phân giác trong và ngoài của góc B, chứng minh MN//BC và MN = AB. c.Chứng minh ABMABC. Tìm tỉ số đồng dạng. Giải: a.Ta có SinC = AB = BCSinC = 10Sin300 = 10. = 5 CosC = AC = BCCosC = 10.Cos300 = = 5 b.Tứ giác AMBN là hình chữ nhật BOM cân = mà = = 2 góc này ở vị trí so le trong MN//BC và MN = AB (T/c) c. ABMBCA (g.g) Tỉ số đồng dạng K = = = Bài 10: Cho ABC, AA’, BB’, CC’ là các đường cao của ABC a.Chứng minh ACC’ABB’; ABCAB’C’ b.Chứng minh ab’.bc’.ca’ = ab.bc.ca.CosACosBCosC c.Cho = 300, BC = 8cm, AC = 6cm. Tính SABC=? Giải: a. ACC’ABB’ (g.g) = b. ABC và AB’C’ chung = (CMT) ABCAB’C’ c.Xét vABB’có CosA = AB’ = ABCosA vACA’ có CosC = CA’ = ACCosC vAA’B có CosB = BC’ = CBCosB AB’.CA’.BC’ = AB.AC.CBCosACosBCosC * SinC = AA’ = ACSin300 = 6Sin300 = 6. = 3cm SABC = AA’.BC = .3.8 = 12cm2 Bài tập tương tự Bài 11: Cho ABC vuông ở A, AB = 3cm, AC = 4cm. Gọi H là chân đường cao kẻ từ đỉnh tới cạnh huyền BC và M là trung điểm của BC. Qua M kẻ đường thẳng song song với cạnh AB cắt AC tại D. a.Tính độ dài AH, AM, HM b.Chứng minh ADMAHB c.Giả = a và = b. Chứng tỏ rằng 7Sina = 15Sinb Bài 12: Cho hình bình hành ABCD, góc B = 1200, AB = 2BC. Gọi I là tđ của DC. a.Chứng minh AIB vuông. b.Tính các cạnh, các góc cuả AIB biết chu vi hình bình hành là 60cm. Bài 13: Cho ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm. a.Chứng minh ABC vuông. b.Tính , và đường cao AH. c.Lấy điểm M bất kỳ trên BC. Gọi hình chiếu của M trên AB, AC lần lượt là P và Q. Chứng minh PQ = AM. Hỏi M ở vị trí nào thì PQ có độ dài nhỏ nhất. Bài 14: Cho ABC có AB = 12cm, = 400, = 300. Đường cao AH. Tính AH, AC, CB. Bài 15: Cho ABC vuông ở A. Đường cao AH = 15, BH = 20. Tính AB, AC, BC, HC. Bài 16: Cho ABC vuông ở A, có AB = 5, BC = 7. GiảI vABC Chương II Đường tròn a.Lý thuyết (Tóm tắt Sgk) 1.*Tâm của đường tròn ngoại tiếp v là trung điểm của cạnh huyền. * Nếu một tam giác có 1 cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó vuông. 2.Quan hệ vuông góc giữa đường kính và dây. *Cho (O), đường kính AB, dây CD AB CD tại I IC = ID *Cho (O), đường kính AB AB cắt CD tại I, IC = ID, I0 AB CD 3.Liên hệ giữa dây và khoảng cách từ tâm đến dây. *AB = CD OH = OK *AB > CD OH < OK 4.Dấu hiệu nhận biết tiếp tuyến * Tính chất : d là tiếp tuyến của (O) tại I OI d *Dấu hiệu: Cho (O), I (O) OI d tại I d là tiếp tuyến của (O) .Tính chất 2 tiếp tuyến cắt nhau *Cho (O): AB,AC là 2 tiếp tuyến cắt nhau tại A(B,C là các tiếp điểm) AB = AC; AO là phân giác của ; OA là phân giác của 6.Tính chất đường nối tâm *Cho (O) cắt (O’) tại A và B. OO’ là trung trực của AB *Cho (O) tiếp xúc (O’) tại I I OO’ B.Bài tập: Bài 1:Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. a.Chứng minh rằng các điểm A, B, C, D cùng thuộc đường tròn. Chỉ ra vị trí tâm đường tròn đó. b.Tính bán kính của đường tròn đó. Giải: -Xét ABD có = 900 (gt) ABD vuông tại A Gọi O là tđ của BD (O) ngoại tiếp ABD (1) Chứng minh tương tự ta có (O) ngoại tiếp DBC (2) Từ (1) và (2) A, B, C, D cùng thuộc (O), tâm O là tđ của DB. - áp dụng định lý Pitago tính DB = ? Bài 2: Cho hình vuông ABCD a.Chứng minh A, B, C, D cùng thuộc đường tròn, chỉ ra vị trí tâm đường tròn. b.Tính bán kính đường tròn đó biết cạnh hình vuông bằng 2dm. Bài 3: Cho ABC nhọn, vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự tại D và E. a.Chứng minh CD AB, BE AC. b. Gọi K là giao điểm của BE và CD. Chứng minh rằng AK BC Giải: Ta có (O) ngoại tiếp BDC O là tđ của BC DBC vuông tại D CD AB Chứng minh tương tự BE AC Xét ABC Có DC AB CD là đường cao ABC BE AC(gt) BE là đường cao ABC CD cắt BE tại K (gt) K là trực tâm của ABC AK là đường cao AKBC Bài 4: Cho ABC cân tại A, nội tiếp O đường cao AH cắt (O) tại D. a.Vì sao AD là đk b.Tính c.Cho BC = 24cm, AC = 20cm. Tính AH và bk (O) Giải: a.Xét ABC cân tại A có AH là đường cao AH đồng thời là đường trung tuyến HB = HC O thuộc AH hay AD là đk của (O) b.Ta có (O) ngoại tiếp ADC (gt) O là tđ của AD (CMT) ADC vuông tại C = 900 c.HC = BC = 12cm áp dụng định lý Pitago cho vAHC AH = ? áp dụng hệ thức lượng cho vADC ta có: HC2 = AH.HD HD = ? AO = AD = Bài 5: Cho ABC, < 900, các đường cao BD, CE. Gọi M và N theo thứ tự là tđ của BC, DE. a.CMR: 4 điểm B, E, D, C cùng thuộc đường tròn. b.Chứng minh DE < BC c.Chứng minh MN ED d. ABC có thêm đk gì thì MDE là tam giác đều Giải: a. BCD vuông tại D M là tđ của BC (M) ngoại tiếo BCD Tương tự (M) ngoại tiếp BEC B, C, D, E thuộc đường tròn tân M b.Ta có BC là đường kính (M) ED là dây của đường tròn (M) M ED ED < BC c.Ta có N là tđ của dây ED(gt) NM MN ED Bài 6: Cho (O), đkính AD = 2R. Vẽ cung tâm D bán kính R cung này cắt đường tròn (O) ở B và C a.Tứ giác OBDC là hình gì? Vì sao? b.Tính số đo các góc , , c.CMR ABC là tam giác đều Giải: a.Xét tứ giác OBDC có OB = BD = DC = OC = R OBDC là hình thoi BC là phân giác của (T/c) b. OBD đều = 600 (T/c) = = 600 = 300 = Ta có (O) ngoại tiếp ABD Có AD là đường kính (O) ABD vuông tại B = 900 = - = 900 – 600 = 300 c.XétABC có = = 600 ABC đều Bài 7: Cho nửa (O), đường kính AB. Qua điểm C thuộc nửa đường tròn kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. CMR: a.CE = CF b. AC là phân giác góc BAE c.CH2 = AE.BF. Giải: a.Ta có: AE//OC//FB Xét àEB có AE//BF (CMT) AEFB là hình thang Có b. AOC cân tại O = (T/c) = (SLT) = AC là phân giác của c.O ngoại tiếp ABC AB là đường kính (O) ABC vuông tại C, có CH AB(gt) CH2 = AH.HB (1) Ta có vAEC = vAHC (Huyền – góc nhọn) AE = AH (Cạnh tương ứng) (2) Ta có v CFB =v CHB HB = BF (Cạnh tương ứng) (3) Từ (1), (2), (3) CH2 = AE.BF Bài 8: Cho đường tròn (0, 3cm), và điểm A có AO = 5cm. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Gọi H là giao điểm của AO và BC. a.Tính độ dài OH b.Qua điểm M bất kỳ thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn cắt AB, AC theo thứ tự tại D và E. Tính chu vi ADE Giải: a. OBC cân có OA là phân giác (T/c) OA là đường cao OA BC tại H Xét v OBA có BH AO OB2 = OH.OA OH = = = b.PADE = AB + DE + AE = AD + HD + HE + AE Mà HD = BD (T/ c) HE = CE (T/c) PADE = AD + DB + CE + EA = AB + CA (mà AB = AC (T/c)) PADE = 2AB áp dụng Pitago chov OBA AB = ? Bài 9: Cho đường tròn (O), bán kính R. Một điểm M ngoài đường tròn cách (o) một khoảng bằng 2R. Kẻ 2 tiếp tuyến MA, MB (A, B là các tiếp điểm). Từ O kẻ đường vuông góc với AO cắt MB tại C a.Chứng minh CM = CO b. Gọi giao điểm MO với đường tròn (O) là I. Chứng minh CI là tiếp tuyến của (O) Giải: a.Ta có AM, BM là 2 tiếp tuyến của (O) cắt nhau tại M = (T/c) Ta có MA là tiếp tuyến của (O) MA OA (đ/l) Có OC OA(g/t) MA//OC = (SLT) = (cùng = ) OMC cân tại C OC = CM b.Xét OCM cân tại C, có OI = IM CI là đường trung tuyến CI đồng thời là đường cao (T/c) CI OI Vậy CI là tiếp tuyến của (O) Bài 10: Cho đường tròn tâm (O), đường kính AB = 2R. Gọi Ax , By là các tiếp tuyến của đường tròn. Qua điểm E thuộc đường tròn kẻ tiếp tuyến thứ 3 cắt Ax tại M và cắt By tại N. a.Chứng minh = 900 b.Chứng minh AM + BN ... = AF.AC AE.AB = AF.AC c.Hình chữ nhật AEHF nội tiếp = (góc nội tiếp cùng chắn ) mà AH là tt của (O) = (góc nội tiếp và góc tạo bởi tt cùng chắn ) = mà + = 1800 (kề bù) + = 1800 Tứ giác BEFC nội tiếp Bài 6: Cho ABC nhọn. Vẽ đường tròn (O) đường kính BC cắt AB tại K và AC tại H. BH cắt CK tại I. a.Chứng minh AI BC b.AI cắt BC tại D. Chứng minh tứ giác BKID nội tiếp. c.Chứng minh CK là phân giác của góc và I là tâm đường tròn nội tiếp DKH Giải: a.Ta có: = 900 (góc nội tiếp chắn nửa (O)) = 900 (góc nội tiếp chắn nửa (O)) CK, BH là 2 đường cao của ABC cắt nhau tại I. I là trực tâm AI là đường cao của ABC AI BC b. = 900 + = 900 + 900 = 1800 BKID nội tiếp c.Ta có = (góc nội tiếp cùng chắn của.....) = (góc nội tiếp cùng chắn của (O)) = KC là phân giác Chứng minh tương tự ta có HB là phân giác của KC và HB cắt nhau tại I I là tâm đường tròn nội tiếp KHD Bài 7: Cho (0, R) 2 đường kính AB, CD vuông góc với nhau. Gọi M là TĐ cuảu CO, N là giao điểm của AM với đường tròn tiếp tuyến với đường tròn tại N cắt đường trung trực của CO tại I. CMR: a. OMNB, OMNI nội tiếp b.AM.AN = AO.AB = 2R2 c. AMIO là hình bình hành Giải: a.Ta có = 900 (góc nội tiếp chắn nửa (0)) = 900 (gt) + = 900 +900 = 1800 OMNB nội tiếp b.Xét AMOABN(g.g) = AM.AN = AO.AB (AO = R, AB = 2R) = 2R2 Chứn minh OMNI nội tiếp ta có = 900 (gt) và = 900 (vì NI là tt của (0)) = = 900 M, N cùng nhìn xuống 2 đầu mút của đoạn IO dưới 1 góc bằng 1v không đổi M, N đường tròn đường kính IO OMNI nội tiếp c.MI//AO (cùng CD) ta có = (góc đáycân ANO ) = (góc nội tiếp cùng chắn .....) = Xét vAMO có + = 900 Xét vOMI có + = 900 = mà 2 góc này ở vị trí so le trong AM//OI AMIO là hình bình hành Bài 8:Cho điểm A nằm ngoài (O, R). Từ A vẽ tiếp tuyến AB, AC và cát tuyến ADE đến (O). Gọi H là TĐ của DE. a.Chứng minh A, Chứng minh AB2 = AI.AH d.Cho AB = R và OH = . Tính HI theo R Giải: a.Ta có = = = 900 B, C, H cùng nhìn xuống 2 đầu mút của đoạn AO dưới một góc bằng 1v không đổi. B, H, C cùng thuộc đường tròn đường kính OA b.Ta có AB = AC(tính chất 2 tt cắt nhau) = = (góc nội tiếp cùng chắn 2 cung = ) HA là phân giác của c.Xét ABI và AHB có chung = (góc nội tiếp cùng chắn 2 cung = ) ABI AHB (g.g) = AB2 = AI.AH d.XétvOBA ta có AO2 = OB2 + BA2 = R2 + 3R2 =4R2 OA = 2R Xét OHA vuông tại H ta có HA2 = OA2 - OH2 = 4R2 - = HA = Ta có AB2 = AH.AI (CMT) AI = = AI = = = HI = AH - AI = - = HI = Bài 9: Cho ABC cân tại A nội tiếp (O). Tia phân giác của cắt AB ở M cắt (O) ở E. Tia phân giác của cắt AC ở N, cắt (O) ở D. a.Chứng minh BCEMBE và EB2 = ME.EC b.Chứng minh MN//BC c.Chứng minh B, C cùng nhìn xuống 2 đầu mút của đoạn MN dưới 2 góc bằng nhau B, M, N, C cùng đường tròn Chứng minh tương tự ta có mà = (góc nội tiếp cùng chắn của....) = (2 góc này ở vị trí so le trong) MN//BC c.Ta có: = (CMT) mà = (góc nội tiếp cùng chắn ) = mà + = 1800 (kề bù) + = 1800 EMND nội tiếp Bài 10: Cho cân tại A, nội tiếp (O). AHBC. Kẻ đường kính BB' và từ A kẻ đường thẳng ADBB' (DBB'), biết BC = 6cm, AH = 4cm. a.Chứng minh ABHD nội tiếp và DH//AB b.Tính DH Giải: a.Xét ABHD có = = 900 D, H thuộc đường tròn đường kính AB ABHD nội tiếp Ta có: = (góc nội tiếp cùng chắn ) BAO cân tại O = = (2 góc ở vị trí so le trong) HD//AB b.OHBC(gt) BH = BC = 3cm Xét vABH có AB2 = BH2 + AH2 = 9 + 16 = 25 AB = 5cm Ta có ABHD nội tiếp đường tròn có DH//AB ABHD là hình thang cân BD = AH = 4cm XétvABB' có ADBB' (gt) AB2 = BD.BB' 52 = 4.BB' BB' = = 6,25 OA = = Xét OBA có HD//AB = = = = = = 25 HD + 125 = 160 25 HD = 35 HD = = = 1,4 cm Bài 11: Cho (O), đường kính AB. Một cát tuyến MN quay quanh trung điểm H của OB. Gọi I là trung điểm của MN. Từ A kẻ tia AxMN tại K. Gọi C là giao của Ax với BI. a.Chứng minh BN//MC b.Chứng minh OIKC là hình chữ nhật c.Tiếp tuyến Bt với (O) ở B cắt AM tại E cắt Ax tại F. Gọi D là giao điểm thứ 2 của Ax với (O). Chứng minh DMEF nội tiếp Giải: a.Xét CMBN có I là trung điểm của MN (1) Xét ACB có IM = IN (gt); OI là đường kính OI MN ACMN(gt) OI//AC; OA = OC (bán kính (O)) I là trung điểm của CB (2) Từ (1) và (2) CMBN là hình bình hành CM//BN b.Xét OCB có OH = OB (gt) IC = IB (CMT) HI là đường trung bình của OCB HI//OC IK//OC Ta có: OI//CK (CMT) OIKC là hình bình hành có = 900 OIKC là hình chữ nhật c.Ta có = (Sđ - Sđ) (góc có điểm ngoài đường tròn) = Sđ = Sđ (góc nội tiếp chắn) = mà + = 1800 (kề bù) + = 1800 DMEF nội tiếp Bài 12: Cho nửa (O), đường kính CD và A (O). Từ A kẻ đường thẳng song song với CD. Từ D kẻ đường thẳng song song với AC. Hai đường thẳng này cắt nhau tại B. Kẻ AHCB. a.Chứng minh A, B, D, H cùng thuộc đường tròn b.Gọi E là giao của Cb với nửa đường tròn Chứng minh BC.AE = AB.AD Giải: a.Ta có = 900 (góc nội tiếp chắn nửa đường tròn (O)) = = 900 H, D nhìn xuống AB dưới một góc bằng 1v không đổi Vậy H, D cùng thuộc đường tròn đường kính AB H, D, A, B cùng thuộc đường tròn b.Xét ACB và EDA = (góc nội tiếp cùng chắn ) = (góc nội tiếp cùng chắn ) mà = (SLT) = ACB EDA (g.g) AB.AD = AE.CB Bài 13: Cho (O, R) đường kính AB cố định, CD là đường kính di động (CDAB) và CD không vuông góc với AB a.Chứng minh ACBD là hình chữ nhật b.Các đường thẳng BC, BD cắt t2 tại A của đường tròn (O) lần lượt tại E và F. Chứng minh CDEF nội tiếp c. Chứng minh AC.AD = CE.DF Giải: a.Xét ACBD = = = 900 (góc nội tiếp chắn nửa (O)) ACBD là hình chữ nhật b.Ta có = (Sđ - Sđ) = Sđ (góc ngoài đường tròn (O) tại E) Ta có = Sđ (góc nội tiếp chắn ) = mà + = 1800 + = 1800 CDEF nội tiếp c.Xét ADF và ECA có = (SLT) = (SLT) ADF ECA (g.g) AD.AC = CE.DF Bài 14: Cho tứ giác ABCD nội tiếp đường tròn (O), đường kính BD, các đường chéo AC và BD cắt nhau ở E. Biết AB = BC = 4cm, = 600 a.Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA của tứ giác ABCD. Chứng minh tứ giác MNPQ là hình chữ nhật b.Tính độ dài đường kính BD c.Xác định điều kiện của ABCD để tứ giác MNPQ là hình vuông Giải: a. Ta có ABD cân tại B BD là đường kính BD là đường trung trực của AC BDAC - Từ tính chất đường trung bình MNPQ là hình bình hành - Chứng minh = 1v MNPQ là hình chữ nhật b.Ta có: = 1800 - = 1800 - 600 = 1200 = 600 = 1v (góc nội tiếp chắn nửa (O)) Xét vBAD có Cos = BD = BD = = 8cm c.Tứ giác MNPQ là hình vuông MN = MQ AC = BD mà ACBD Khi AC và BD là 2 đường kính tức là tứ giác ABCD là hình vuông thì tứ giác MNPQ là hình vuông. Bài 15: Cho có 3 góc nhọn nội tiếp (O, R), các đường cao AD, BE cắt nhau tại H (DBC, E AC, AB < AC) a.Chứng minh AEDB, CDHE nội tiếp b.Chứng minh CE.CA = CD.CB và DB.DC = DH.DA c.Đường phân giác trong AN của của cắt BC tại N, cắt (O) tại K (KA). Gọi I là tâm của đường tròn ngoại tiếp ACN. Chứng minh KO và CI cắt nhau tại một điểm (O) Giải: a.Tự chứng minh b.Xét CAD và CBE có chung (góc nội tiếp cùng chắn của đường tròn nội tiếp AE, DB) CAD CBE (g.g) CA.CE = CB.CD - Chứng minh BDH ADC (g.g) BD.DC = AD.DH c. (góc nội tiếp -góc ở tâm) Bài 16: Trên đường tròn (O, R) đường kính AB lấy 2 điểm M, E theo thứ tự A, M, E, B (hai điểm M, E A, B). AM cắt BE tại C, AE cắt BM tại D. a.Chứng minh MCED nội tiếp và CD AB b.Gọi H là giao của CD và AB. Chứng minh BE.BC = BH.BA c.Chứng minh các t2 tại M và E của (O) cắt nhau tại 1 điểm nằm trên CD d. Cho = 450 và = 300. Tính SABC theo R Giải: a.Hs tự chứng minh b. BAEBHC (g.g) BE.BC = BH.BA c.IC = IM = ID = IE = = mà = , = mà + = 900 + = 900 = 900 MI là t2 của (O) chứng minh tương tự ta có IE là t2 của (O) MI và IE là 2 t2 cắt nhau tại trung điểm I của CD d. vABETính AE = ? vAECTính AC = ? vCAHTính CH = ? SABC = CH.AB Bài 17: Cho nửa đường tròn (O), đường kính AB. Từ A và B kẻ 2 t2 Ax, By. Qua M nửa đường tròn này kẻ t2 thứ ba cắt các t2 Ax, By lần lượt tại E và F. a.Chứng minh AEMO nội tiếp b.AM cắt OE tại P. BM cắt OF tại Q. Tứ giác MPOQ là hình gì? Tại sao? c.Kẻ MHAB. K là giao điểm của MH và EB. So sánh MK và KH. d.Cho AB = 2R và gọi r là bán kính đường tròn nội tiếp EOF. CMR: = = Giải: a. Hs tự chứng minh b. MPOQ là hình chữ nhật (Hs tự chứng minh) c. Ta có: ME = EA = = ME = EA = EI ta có = mà = = (EA = EI) MK = KH d.Đặt EF = a, EO = b, OF = c Ta có SEOF = r (a + b + c) = Ta có b + c > a < = = Ta có b = = Vậy = = Bài 18: Cho nửa đường tròn (O), đường kính BC. Vẽ dây AB. Gọi I là điểm chính giữa của cung BA, K là giao của OI với BA. a.Chứng minh OI//CA b.Từ A vẽ đường thẳng song song với CI cắt BI tại H. Chứng minh IHAK nội tiếp c.Gọi P là giao của HK và BC. Chứng minh AC.BK = BC.KP (BKP BCA) Giải: a.Hs tự chứng minh b. = = 900 KIHA nội tiếp c. = (đđ) = (nội tiếp chắn ) = (cùng bù ) BKPBCA(g.g) Bài 19: Cho (O), một đường kính AB cố định, một điểm I nằm giữa A và O sao cho AI = AO. Kẻ dây MNAB tại I. Gọi C là điểm tuỳ ý thuộc cung lớn MN sao cho C không trùng với M, N và B. Nối AC cắt MN tại E. a.Chứng minhIECB nội tiếp b.Chứng minh AEMACM và AM2 = AE.AC c.Chứng minh AE.AC - AI.IB = AI2 Giải: a.Hs tự chứng minh b. AEM và ACM có chung, = (cùng chắn 2 cung bằng nhau) AEMACM AM2 = AE.AC c.Ta có vBMA có MI2 = IA.IB AM2 - MI2 = AE.AC - AI.IB = AI2 Bài 20: Cho 3 điểm A, B, C thẳng hàng (B nằm giữa A, C). Vẽ đường tròn tâm O đường kính BC. AT là t2 vẽ từ A. Từ tiếp điểm t vẽ đường thẳng BC, đường thẳng này cắt BC tại H và cắt đường tròn tại T'. Đặt OB = R a. Chứng minh OH.OA = R2 b. Chứng minh TB là phân giác của c.Từ B vẽ đường thẳng // TC. Gọi D và E lần lượt là giao điểm của đường thẳng vừa vẽ với TT' và TA. Chứng minh TED cân d.Chứng minh = Giải: a.Các câu a, b, c Hs tự chứng minh d.Xét ATC có EB//TC = (Hệ quả Talet) THC có BH//TC = (Hệ quả Talet) Mà EB = BH (CMT) = Bài 21: Cho (O, R) và 1 điểm S ở ngoài đường tròn vẽ 2 t2 SA, SB, vẽ đt a đi qua S và cắt đường tròn (O) tại M và N (M nằm giữa S, N), a không đi qua O a.Chứng minh OSAB b.Gọi H là giao của SO và AB. I là trung điểm của MN, 2 đt OI và AB cắt nhau tại E. Chứng minh IHSE nội tiếp c.Chứng minh OI.OE = R2 d.Cho OS = 2R và MN = R.Tính SESM theo R. Giải: a, b: Hs tự chứng minh c. OI.OE = OH.OS = R2 d.Tính OI (dựa vONI) Tính SI (dựavOIS) Tính MS = IS - IM Tính OE dựa vào câu c SEMS = EI.MS Bài 22: Cho đường tròn (O) đường thẳng d không đi qua (O) và cắt đường tròn tại 2 điểm A và B. Từ 1 điểm C trên d (C nằm ngoài đường tròn) kẻ 2 tiếp tuyến CM, CN với đường tròn (M, N (O)). Gọi H là trung điểm của AB, đt OH cắt CN tại K. a.Chứng minh 4 điểm C, O, H, N đường tròn b.Chứng minh KN.KC = HK.KO c.Đoạn thẳng CO cắt đường tròn (O) tại I. Chứng minh I cách đều CM, CN, MN d.Một đt đi qua O và song song với MN cắt các tia CM, CN lần lượt tại E và F. Xác định vị trí của C trên d sao cho diện tích CEF nhỏ nhất.
Tài liệu đính kèm:
 On tap hinh hoc 9.doc
On tap hinh hoc 9.doc





