Đề thi học sinh giỏi lớp 9 môn: Toán
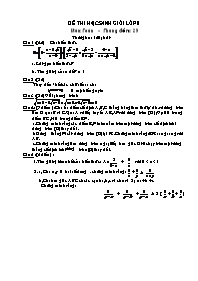
Câu 1 :(4đ) Cho biểu thức
a. Rút gọn biểu thức P
b. Tìm giá trị của x để P = 1
Câu 2 :(2đ)
Thay dấu * bởi các chữ số sao cho
là một số nguyên
Câu 3 :(2đ) Giải phương trình
Câu 4: (7 điểm ) :Cho ba điểm cố định A,B,C thẳng hàng theo thứ tự đó.vẽ đường tròn tâm O qua B và C.Qua A vẽ tiếp tuyến AE,AF với đường tròn (O); Gọi I là trung điểm BC ,N là trung điểm EF .
a.Chứng minh rằng các điểm E,F luôn nằm trên một đường tròn cố định khi đường tròn (O) thay đổi .
b.Đường thẳng FI cắt đường tròn (O) tại K .Chứng minh rằng :EK song song với AB .
c.Chứng minh rằng tâm đường tròn ngoại tiếp tam giác ONI chạy trên một đường thẳng cố định khi đường tròn(O) thay đổi.
Bạn đang xem tài liệu "Đề thi học sinh giỏi lớp 9 môn: Toán", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Đề thi học sinh giỏi lớp 9 Môn: Toán - Thang điểm: 20 Thời gian : 150 phút Câu 1 :(4đ) Cho biểu thức a. Rút gọn biểu thức P b. Tìm giá trị của x để P = 1 Câu 2 :(2đ) Thay dấu * bởi các chữ số sao cho là một số nguyên Câu 3 :(2đ) Giải phương trình Câu 4: (7 điểm ) :Cho ba điểm cố định A,B,C thẳng hàng theo thứ tự đó.vẽ đường tròn tâm O qua B và C.Qua A vẽ tiếp tuyến AE,AF với đường tròn (O); Gọi I là trung điểm BC ,N là trung điểm EF . a.Chứng minh rằng các điểm E,F luôn nằm trên một đường tròn cố định khi đường tròn (O) thay đổi . b.Đường thẳng FI cắt đường tròn (O) tại K .Chứng minh rằng :EK song song với AB . c.Chứng minh rằng tâm đường tròn ngoại tiếp tam giác ONI chạy trên một đường thẳng cố định khi đường tròn(O) thay đổi. Câu 5 :(5điểm ) : 1.Tìm giá trị lớn nhất của biểu thức : A= + với 0 < x <1 2. a, Cho x,y là hai số dương . chứng minh rằng : + b,Cho tam giác ABC có các cạnh a,b,c và chu vi 2p =a+ b + c Chứng minh rằng : + + 2 ( + + ) đáp án và thang điểm câu Nội dung Điểm 1a. đk 0,5 Ta có: 0,5 = 0,5 = 0,5 = Vậy P = 0,5 b. Ta thấy P = 1 0,5 0,5 Vậy với x = 25 thì P = 1 0,5 2 đặt thì x5 = *****4 0,5 x tận cùng bởi 4 0,5 Lại có 10 < x < 20 vì 105 =100000<*****4 <32.100000=205 0,5 Do đó x=14 và x5 = 145 =537824 0,5 3 (điều kiện x) 0,25 += 5 0,25 (*) 0,25 -trường hợp 0,25 thì thoả mãn điều kiện x 0,25 - trường hợp 0,25 (*) phương trình nghiệm đúng với mọi x 0,25 kết hợp cả 2 trường hợp ta có tập nghiệm của phương trình là x 0,25 Câu4 a ABFvà AFC đồng dạng (g_g) 0.5đ Ta có :AB/ AF=AF/ACAF2=AB.AC 0.5đ AF= Mà AE=AF nên AE=AF= không đổi 0.5đ Vậy E,F thuộc đường tròn (A;) cố định. 0.5đ b Tứ giác AOIF nội tiếp đường tròn Ta có :AIF =AOF (1) AOF = EOF và EKF =EOF 0.5đ EKF =AOF (2) 0.5đ Từ(1) và(2) AIF =EKF 0.5đ Do đó :EK vàAB song song vơí nhau 0.5đ c Cm được A,N,O thẳng hàng và AOEF ; Gọi H là giao điểm của BC và EF Ta có : ANH và AIO đồng dạng nên 0.5đ Suy ra :AH.AI =AN.AO Lại có :AN .AO=AE2 =AB.AC 0.5đ Do đó : AI.AH =AB.AC không đổi . Vậy H cố định 1đ Tứ giác OIHN là tứ giác nội tiếp đường tròn nên đường tròn ngoại tiếp OIN luôn qua I và H ;Do đó tâm đường tròn này nằm trên đường trung trực của IH 1đ câu5 1 (với 0 <x < 1) 0.5đ áp dụng bất đẳng thức Cauchy với hai số dươngvà ta có 0.5đ Dấu “=” xãy ra khi và chỉ khi : 0.5đ Vậy min A = khi 0.5đ 2a cho x>0, y>0 ta có 0.5đ dấu “=” xảy ra khi và chỉ khi: x- y = 0 hay x=y Vậy: dấu “=” xảy ra khi và chỉ khi: x=y 0.5đ b, ta có: 0.5đ áp dụng bất đẳng thức: x, y>0 ta có: 0.5đ Tương tự ta có: ; 2 0.5đ Dấu “ =” xảy ra khi và chỉ khi: a=b=c 0.5đ ý kiến ban thẩm duyệt Quan hoá, ngày 12 tháng 4 năm 2011 Người ra đề Hà Lệ Thảo
Tài liệu đính kèm:
 de thi hsg.doc
de thi hsg.doc





