Giáo án môn Hình học khối 9 - THCS Lương Định Của - Tiết 18: Kiểm tra chương I
Bài 1 (2 điểm). Bài tập trắc nghiệm.
Khoanh tròn chỉ một chữ đứng trước câu trả lời đúng.
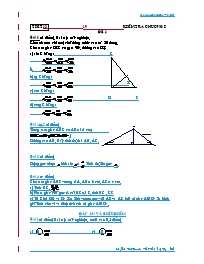
Cho tam giac DEF có = 900, đường cao DI.
a) sin E bằng : E
b) tg E bằng :
I
c) cos F bằng :
D F
d) cotg F bằng :
Bài 2 (2 điểm)
Trong tam giác ABC có AB = 12 cm;
;
Đường cao AH. Hãy tính độ dài AH, AC.
Bài 3 (2 điểm)
Dựng góc nhọn biết sin = . Tính độ lớn góc .
Bạn đang xem tài liệu "Giáo án môn Hình học khối 9 - THCS Lương Định Của - Tiết 18: Kiểm tra chương I", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
TIẾT 18 19 KIỂM TRA CHƯƠNG I ĐỀ 1 Bài 1 (2 điểm). Bài tập trắc nghiệm. Khoanh tròn chỉ một chữ đứng trước câu trả lời đúng. Cho tam giac DEF có = 900, đường cao DI. a) sin E bằng : E b b) tg E bằng : I c) cos F bằng : D F d) cotg F bằng : Bài ) tg2 (2 điểm) Trong tam giác ABC có AB = 12 cm; ; Đường cao AH. Hãy tính độ dài AH, AC. Bài 3 (2 điểm) Dựng góc nhọn biết sin = . Tính độ lớn góc . Bài 4 (4 điểm) Cho tam giác ABC vuông ở A, AB = 3 cm, AC = 4 cm. a) Tính BC, b) Phân giác của góc A cắt BC tại E. tính BE , CE c) Từ E kẻ EM và EN lần lượt vuông góc với AB và AC. hỏi tứ giác AMEN l;à hình gì? Tính chu vi và diện tích của tứ giác AMEN. ĐÁP ÁN VÀ BIỂU ĐIỂM Bài 1(2 điểm) Bài tập trắc nghiệm. (mỗi câu 0,5 điểm) a) B c) B b) B d) C Bài 2 (2 điểm) AH = 12 . sin 400 7,781 (cm) 1 điểm 1 điểm Bài 3 ( 2 điểm) Hình dựng đúng 1 điểm A 1 5 2 O B Cách dựng. Chọn một đoạn thẳng làm đơn vị Dựng tam giác vuông OAB có : Có = 0,5 điểm Chứng minh : sin = sinOBA = => 0,5 điểm Bài 4 (4 điểm) Hình vẽ đúng 0,25 điểm a) (đ/l Pytago) 0,75 điểm 0,75 điểm 0,25 điểm b) AE là phân giác góc  0,5 điểm Vậy EB = EC = 0,5 điểm c) Tứ giác AMEN có => AMEN là hình chữ nhật có đường chéo AE là phân giác góc A => AMEN là hình vuông. 0,5 điểm Trong tam giác vuông BME ME = BE sinB 1,71(cm) Vậy chu vi AMEN 6,68 (cm) Và diện tích AMEN 2,94 (cm) 0,5 điểm ĐỀ 2 \Bài 1(2 điểm). Bài tập trắc nghiệm. a) Chọn kết quả đúng trong các kết quả dưới đây bằng cách khoanh tròn chữ cái đứng trước. Cho hình vẽ 1) sin bằng A. 2) tg bằng 12 13 A. b) Đúng hay sai? Cho góc nhọn sin2 = 1 – cos2 0 < tg < 1 sin= cos = sin(900 - ) Bài 2 (2 điểm) Cho tam giác ABC vuông tại A, đường cao AH. Cho AH = 15; BH = 20. tính AB, AC, BC, HC A 15 B 20 H C Bài 3 ( 2 điểm) Dựng góc nhọn biết cotg= Tính độ lớn của góc Bài 4 (4 điểm) Cho tam giác ABC có AB = 6 cm ; AC = 4, 5cm; BC = 7,5cm. Chứng minh ABC là tam giác vuông. Tính và đường cao AH Lấy M bất kỳ trên cạnh BC. Gọi hình chiếu của của M trên AB, AC lần lượt là P và Q. chứng minh PQ = AM. Hỏi M ở vị trí nào thì PQ có độ dài nhỏ nhất? ĐÁP ÁN VÀ BIỂU ĐIỂM Bài 1 (2 điểm). Bài tập trắc nghiệm. a) 1.C 0,5 điểm A 0,5 điểm b) 1) Đúng 0,25 điểm 2) Sai 0,25 điểm 3) Sai 0,25 điểm 4) Đúng 0,25 điểm Bài 2 (2 điểm) A 15 B 20 H C AB = 0,5 điểm AB2 = BC . BH => BC = BC = 0,5 điểm HC = BC – BH = 31,25 – 20 = 11,25 0,5 điểm AB. AC = BC . AH => AC = AC = AC = 18,75 0,5 điểm Bài 3 (2 điểm) Hình dựng đúng 1 điểm Cách dựng : Chọn một đoạn thẳng làm đơn vị. Dựng tam giác uong AOB có Ô = 900, OA = 3 , OB = 4 Có . 0,5 điểm Chứng minh : cotg = cotgOAB = => 0,5 điểm Bài 4 (4 điểm) Hìønh vẽ đúng. 0,25 điểm a) AB2 + AC2 = 62 + 4,52 = 56,25 BC2 = 7,52 = 56,25 => AB2 + AC2 = BC2 (=56,25) 1 điểm Vậy ABC vuông tại A theo định lý đảo Pytago b) sin B = => 36052/ 0,25 điểm BC . AH = AB . AC => AH = 0,75 điểm c) Tứ giác APMQ có => APMQ là hình chữ nhật Trong hình chữ nhật hai đường chéo bằng nhau : PQ = AM 0,5 điểm Vậy PQ nhỏ nhất ĩ AM nhỏ nhất. ĩ AM BC ĩ M H
Tài liệu đính kèm:
 T.19 - Kiem tra chuong I.doc
T.19 - Kiem tra chuong I.doc





