Đề kiểm tra học kì II môn Toán Lớp 9 - Đề số 4 (Có đáp án)

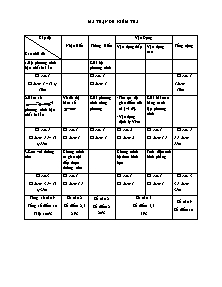
MA TRẬN ĐỀ KIỂM TRA 
 Cấp độ 
Các chủ đề 
Nhận Biết
Thông Hiểu
Vận Dụng 
Tổng cộng
Vận dụng thấp 
Vận dụng cao 
1.Hệ phương trình bậc nhất hai ẩn 

Giải hệ phương trình 



Số câu 1
Số điểm 1 – Tỉ lệ 10%

Số câu 1
Số điểm 1	 


Số câu 1
 1điểm =10% 
2.Hàm số và phương trình bậc nhất hai ẩn 
Vẽ đồ thị hàm số 
Giải phương trình trùng phương 
Tìm tọa độ giao điểm của (d ) và (P).
Vận dụng định lý Vi-ét
Giải bài toán bằng cách lập phương trình 

Số câu 5
Số điểm 5,5– Tỉ lệ55%
Số câu 1
Số điểm 1	 
Số câu 1
Số điểm 1	 
Số câu 2
Số điểm 2	 
Số câu 1
Số điểm 1,5	 
Số câu 5
5,5 điểm= 55%
3.Góc với đường tròn 
Chứng minh tứ giác nội tiếp được đường tròn 

Chứng minh hệ thức hình học 
Tính diện tích hình phẳng 

Số câu3
Số điểm 3,5– Tỉ lệ35%
Số câu 1
Số điểm 1,5	 

Số câu 1
Số điểm 1	 
Số câu 1
Số điểm 1	 
Số câu 3
3,5 điểm= 35%
Tổng số câu 9
Tổng số điểm 10
 Tỉ lệ 100%
Số câu 2
Số điểm 2,5
25%
Số câu 2
Số điểm 2 20%
Số câu 5
Số điểm 5,5
55%
Số câu 9
Số điểm 10 

ĐỀ KIỂM TRA 
Bài 1: ( 3 điểm) ( Không dùng máy tính cầm tay )
Giải hệ phương trình:
Giải phương trình:
Cho phương trình bậc hai:
	(m là tham số )
	Tìm m để phương trình có hai nghiệm thỏa mãn 
Bài 2: (1,5 điểm)
Một tam giác vuông có chu vi bằng 30m, cạnh huyền bằng 13m. Tính mỗi cạnh góc vuông.
Bài 3: ( 2 điểm)
Trong mặt phẳng tọa độ cho prabol( P): 
Vẽ đồ thị ( P )
Bằng phương pháp đại số tìm tọa độ giao điểm A và B của (P) và đường thẳng (d): 
Bài 4: (3,5điểm)
Từ điểm A ở ngoài đường tròn (0;2cm). Kẻ hai tiếp tuyến AB, AC và cát tuyến AMN với đường tròn đó (M nằm giữa A và N), cho góc BAC có số đo bằng 600. 
Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm và bán kính của đường tròn ngoại tiếp tứ giác ABOC.
Chứng minh: 
Tính diện tích phần hình giới hạn bởi các đoạn AB, AC và cung nhỏ BC nói trên.
ĐÁP ÁN VÀ THANG ĐIỂM 
BÀI 
ĐÁP ÁN 
ĐIỂM
1.1
Giải hệ phương trình:
	
1đ
 
0,25đ

0,25đ

0,25đ
Vậy hệ phương trình có một nghiệm duy nhất 
0,25đ
1.2
Giải phương trình:
1đ
Đặt phương trình trở thành 
0,25đ
Giải và (nhận) (nhận)
0,25đ

0,25đ
Vậy phương trình có 4 nghiệm: 
0,25đ
1.3
Tìm m để phương trình có hai nghiệm thỏa mãn 
1đ
Phương trình có nghiệm khi D’
0,25đ
Viết đúng hệ thức Vi-et 
0,25đ

0,25đ
vậy m = 8
0,25đ
2 
Tìm hai cạnh góc vuông
1,5đ
Gọi là cạnh góc vuông thứ nhất. Điều kiện 
0,25đ
Cạnh vuông thứ hai: 
0,25đ
Sử dụng định lý Pitago viết phương trình 
0,25đ

0,25đ
Lập 
0,25đ
(nhận) (nhận)
Vậy độ dài hai cạnh góc vuông là: 12m và 5m 
0,25đ
3
a. Vẽ đồ thị (P): 
1đ
Bảng giá trị


-2
-1
0
1
2



-8
-2
0
-2
-8


0,5đ
Vẽ đúng đồ thị 
0,5đ
b.Tọa độ giao điểm của (P) và (d)
1đ
Phương trình hoành độ giao điểm của (P) và (d) là: 
0,25đ
Giải ra nghiệm 
0,25đ
Tìm được tọa độ giao điểm A(-1;-2) và B()
0,5đ
4

Vẽ hình:
. Tứ giác ABOC có (tính chất của tiếp tuyến )
0,5đ
 Tứ giác ABOC nội tiếp đường tròn 
0,5đ
(tính chất hai tiếp tuyến giao nhau ) và là tam giác đều 
(hai góc nội tiếp cùng chắn cung)

0,25đ
Vậy tứ giác ABOC nội tiếp trung đường tròn tâm là trung điểm của OA bán kính bằng 2 cm.
0,25đ
Xét hai tam giác .
 (góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung )
0,25đ
chung 
0,25đ
Suy ra DABM đồng dạng DANB(g.g)
0,25đ

0,25đ
Tứ giác ABOC nội tiếp 
0,25đ
 Squạt OBMC 
0,25đ

0,25đ
Scần tìm = SOBAC – Squạt 
	
0,25đ

Học sinh giải cách khác đúng vẫn đạt điểm tối đa